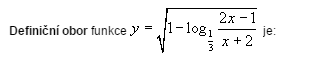Definiční obor funkce
Zdravím. Zasekl jsem se momentálně na příkladě z kurzu scio matematiky -> příklad je jako obrázek v příloze.
Mám určit definiční obor té funkce a je to celé pod odmocninou takže jsem ten celý vnitřek postavil větší nebo rovno nule, začal řešit a vznikla logaritmická nerovnice.
Což o to, logaritmické nerovnice jsou easy ale problém je v tom, že tady jsou minimálně dvě cesty jak to řešit a každá mi dává jiný výsledek - resp. jiný interval.
Já jsem si vnitřek pod tou odmocninou rozložil takto:
pozn.: číslo vedle log je základ, v závorce je argument.
log3(3) + log3(2x-1) - log3(x+2) >= log3(1)
Tohle jsem vyřešil a čistě z této lograitmické nerovnice mi vyšlo, že x musí být z intervalu <1, + ∞)
Problém je, že toto není celé řešení (dle scia). Řešením je můj interval sjednocený s intervalem (-∞, -2).
Toto řešení by vyšlo, pokud bych ten logaritmus s lomeným výrazem v argumentu nerozkládal rozdíl dvou logaritmů což je pro mě jednodušší vyřešit.
Ptám se tedy prosím na radu jak postupovat obecně při řešení podobných příkladů, kde po výběru nevhodného postupu vychází špatné (nebo nekompletní) řešení ...? Pač kdybych tento příklad řešil bez toho rozkladu na dva logaritmy, vyšlo by to dobře - to jsem ale dopředu nemohl vědět.
Díky za radu, Tomáš
Tomáš K.
26. 06. 2017 19:18
4 odpovědi
Ahoj Tomáši, ukážu ti jiný příklad, kde použiju tvůj způsob řešení, takže snadno uvidíš, kde jsi udělal chybu.
Jaký je definiční obor funkce: y = √(x*x-4)
Na základě tvého popisu bys ji řešil takhle:
√(x*x-4) = √((x+2)(x-2) = √(x+2) * √(x-2)
Definiční obor: x >= 2
Podle toho, co píšeš, jsem si jistý, že tu chybí vidíš na první pohled.
Bohužel, stejnou úpravu jsi udělal v případě logaritmů a nevšiml sis toho.
Moje rada zní, zkontroluj si, jestli tvoje úpravy nemění definiční obor.
Pokud máš vnořené funkce a vnější funkce je definovaná pouze pro kladné hodnoty, musíš si dát pozor při násobení a dělení.
Podobný příklad je třeba tahle funkce: y = x
Stejná funkce po úpravě: y = 1 / (1 / x)
Ale vlastně to už stejná funkce není, že?
Tomáš B.
Díky za odpověď.
Tak když bych řešil def. obor y = √(xx-4) tak udělám xx >= 4, odmocním a mám že absolutní hodnota x musí být větší než 2 a to je ok ...
Já chápu že rozdělením toho lomeného výrazu v argumentu toho logaritmu jsem změnil definiční obor té funkce. Ale já jsem přece neurčoval definiční obor toho lomeného výrazu, já jsem prostě jenom řešil logaritmickou nerovnici a věřil jsem tomu, že validním postupem (ať už je jakýkoli) dojdu ke správnému (a jedinému možnému) řešení nerovnice.
Pokud bych teoreticky tento příklad dostal zadaný jako tento výraz:
log3(3) + log3(2x-1) / (x+2) >= log3(1)
a nešlo by mi vůbec o určování nějakého def. oboru tak to stejně vyjde na dvě řešení - jedno pokud bych nechal ten argument jako lomený výraz a něco jiného kdybych to rozdělil na dva logaritmy. To je jediná věc co mě na tom zarazila. Myslel jsem si prostě, že používáním jakéhokoli povoleného postupu vyřeším logaritmickou nerovnici a dostanu pokaždé stejný výsledek. Tady tomu ale očividně tak není a proto jsem se na tom zasekl.
Ahoj Tomáši, začínám tušit, v čem je problém, díky tomu, co jsi napsal.
Cituji, "věřil jsem tomu, že validním postupem dojdu ke správnému řešení nerovnice."
Problém je, že ve škole tě neučí validní postupy, učí tě jenom "postupy".
V matimatice je naprosto běžné něco spočítat špatně a pak to opravit.
Proto také tak často počítáš podmínky a zkoušky - protože postup není validní a je nutné ho opravit.
Až za sebou budeš mít analýzu (a budeš rozumět funkcím) a algebru (a budeš rozumět oborům), poznáš, kdy je postup validní a budeš mít možnost si vybrat, jak úlohu řešit co nejjednodušším způsobem, i jestli je postup validní nebo ne.
Jak ale poznat, že je postup validní?
V tomhle případě nesmíš změnit definiční obor ani obor hodnot vnořené funkce.
Když řešíš logaritmus racionální funkce (tvůj příklad), řekl sis, že je snadnější použít věty o logaritmech, abys pracoval s lineární funkcí.
Ale když řešíš odmocninu kvadratické funkce (můj příklad), řekl sis pro změnu, že je snadnější počítat kvadratickou funkci než lineární?
Tohle je problém, s funkcí zacházíš intuitivně - a takhle to poznat nemůžeš.
Další problém je, že sis myslel, že neurčuješ definiční obor lomeného výrazu, ale opak je pravdou.
Označím si funkce následovně:
f(x) = √(1-x)
g(x) = ln(x)
h(x) = (2x-1)/(x+2)
Ve svém příkladu řešíš definiční obor funkce y = f(g(h(x))) a pro jeho určení musíš postupně pracovat s definičním oborem i oborem hodnot funkcí f, g, h.
Rozdělením racionální funkce pomocí logaritmů jsi změnil obor hodnot funkce h(x), což je přesně ta chyba, která ti unikla.
Pokud po tobě totiž budu chtít najít definiční obor funkce y = F( (2x-1)/(x+2) ), ale neřeknu ti, co je F zač, ani by tě nenapadlo tu úlohu převést na y = F(2x-1) - F(x+2), že ano?
U logaritmů to bereš jako samozřejmé, protože ses tenhle postup naučil - a je to "postup", ne validní postup.
To, že můžeme napsat ln( (2x-1)/(x+2) ) = ln(2x-1) - ln(x+2) ještě neznamená, že je to pravda vždy a všude.
A co s tím?
V první řadě si musíš uvědomit, že nepracuješ s algebraickým výrazem, ale s funkcí.
Některé úpravy výrazů, které znáš, nemůžeš u funkcí použít - nebo můžeš, ale pak musíš zkontrolovat podmínky a zkoušky.
Tím se terpve nepovolený postup zkontroluje a převede na postup povolený.
Zdravím. Díky moc za vysvětlení, už je to jasné. Příště si dám pozor. Přeji hezký zbytek dne