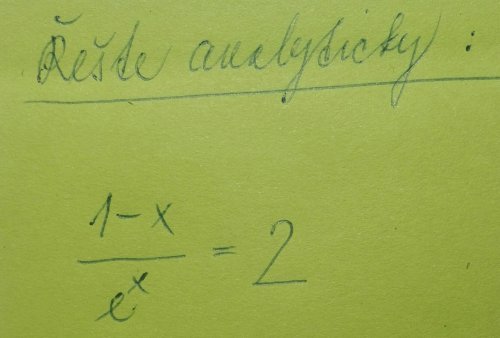Řešení rovnice
7 odpovědí
Dobrý den, Honzo,
zatím mě žádné analytické řešení nenapadá, ale to neznamená, že to nejde. Jenom se zeptám, co studujete? Nebo kdo Vám zadal tenhle příklad? Jde mi o to, jak pokročilou matiku můžu používat....
- ročník MatFyzu
(1 - x) / exp(x) = 2 1 - x = 2 exp(x)
- substituce x=ln(z)
1 - ln(z) = 2z
ln(e / z) = 2z
e / z = exp(2z) 2e = 2z exp(2z)
- substituce y=2z
2e = y exp(y)
A pokud smyslem úlohy není odvodit Lambertovu W funkci, máme tu transcendentální rovnici bez řešení v uzavřeném tvaru.
Analyticky ji tudíž řešit nelze.
Ahoj Tome,
díky moc. K tomu poslednímu řádku jsem se dopracoval taky, ale ten závěr už jsem nevěděl :-).
Ok, děkuji za rady. Dává to smysl. Rovnic v zadání bylo více, ostatní jsem dal dohromady, tady u té tedy nelze analyticky řešit.
Přibližně by šlo bez počítače řešit asi tak, že si narýsuji graf lineární fce y= x-1 a druhé exponenciální fce y= 2.e^x a řešením bude x souřadnice průsečíku grafů fcí.
Děkuji, JM.
Honzo, nedá mi to a nahodím udičku mladému nadějnému matfyzákovi...
Úloha se dá řešit numericky i bez počítače, použije se Newtonova metoda.
- řešíme rovnici: 2 exp(x) + x - 1 = 0
- odhad řešení: x[1] = 0
- iterace: x[i + 1] = x[i] - (2 exp(x) + x - 1) / (2 exp(x) + 1)
Po dvou krocích dostaneme řešení x[3] = -0.374822 platné na 6 desetinných míst.
Jenže počítat exponenciální funkci bez počítače je opruz.
(2 exp(x) + x - 1) / (2 exp(x) + 1) = 1 + (x - 2) / (2 exp(x) + 1) ~ 1 + (x - 2) / (3 + 2x + x^2 + x^3/3)
Takže mám nový iterační vzorec: x[i + 1] = x[i] - (1 + (x - 2) / (3 + 2x + x^2 + x^3/3))
Tentokrát dostanu x[3] = -0.374184 platné na 3 místa.
Děkuji za udičku :) Jak vidím, tak Newtonova metoda je něco na řešení rovnic, jako vzorec pro odmocnění čísla, pokud máme přibližný odhad o velikosti výsledku odmocňování (x) => odmocnina z čísla a = x/2 + a/2x. A po opakování s předchozím lepším odhadem se dostaneme na více a více platných míst.
Píšu si to.
Díky. JM.