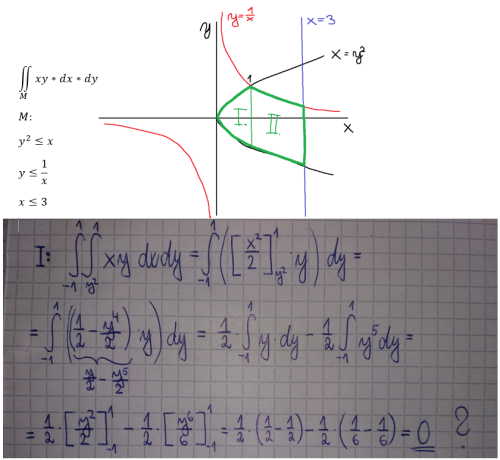
Dvojný integrál
Hezký večer (alespoň pro ty, kdo nemusí po večerech počítat integrály k zápočtu).
Potřeboval bych se vás na něco zeptat.
V příloze je prakticky vše potřebné k pochopení mého dotazu, ale přeci jen to lehce okomentuju.
Logickou úvahou bych řekl, že mým úkolem je spočítat obsah plochy (I.+II.), kterou ohraničují průniky 3 zadaných funkcí (M). První jsem tedy začal počítat oblast I., ke které bych potom přičetl oblast II. Jak je ale možné, že hodnota plochy I. vychází 0?
Je zřejmé, že obsah této oblasti určitě není 0, tak se tedy ptám, co tímto integrálem zjišťuju za "parametr"?
Výpočet by měl být správně..
Mockrát díky, Tomáš.
Tomáš L.
22. 04. 2018 12:11
4 odpovědi
Tomáši, u funkcí více proměnných to chce trochu cviku, než alespoň jednoduché příklady budou "zřejmé".
a) riemannův integrál ∫x dx na intervalu (-1, 1) je roven nule
b) riemannův integrál ∫∫xy dxdy na intervalu x∈(0, 1), y∈(-1, 1) je roven nule
Oba mé příklady jsou jen jednodušší verzí toho, co se snažíš počítat, aby sis mohl zkontrolovat, kde jsi udělal v úvaze chybu.
Výpočet mi na druhou stranu přijde správný.
Doporučuju si v rámci tréninku zkusit představit funkci (b), je to taková "vrtulka".
Díky za odpověď,
ale bohužel mi to stále není jasné...
Proto bych vás chtěl ještě poprosit o zodpovězení těchto otázek:
- Mým výše popsaným výpočtem oblasti I. počítám obsah plochy?
- Pokud ano, jak tedy může vyjít 0? Nulová plocha přece nedává smysl.
Vím, že jednoduchým integrálem počítám obsah (plochu) pod křivkou. U dvojných integrálů se ale (co vím) počítá obsah integrací "jedničky". To je důvod, proč nejsem schopen přijít na to, co je vlastně ta hodnota (v mém případě 0), kterou integrací vypočítám.
Možná v tom akorát zmatkuju, ale aktuálně si v tom nejsem schopen udělat jasno. Děkuji tedy za trpělivost a případnou odpověď. Díky
Když nad tím teď ještě dodatečně přemýšlím, tak kdybych na to šel ještě jinak..a spočítal si obsah poloviny té oblasti I. a pak to vynásobil 2x (protože ta parabola je symetrická kolem osy x), tak by mi to přece nedalo výsledek 0, ne?
To odečtení se na nulu mi prostě hlava nebere..
Určitý integrál se nazývá míra a je to zobecnění pojmů délky, obsahu a objemu, které už znáš ze základní školy.
Na spočítání délky úsečky v euklidovském prostoru stačí Pythagorova věta.
Ale na spočítání délky stejnosměrně spojité křivky už vzorec není a tady nastupuje integrál.
V zadání máš spočítat objem pod křivkou, která je daná funkcí f(x, y) = xy
To je reálná funkce dvou proměnných, jejím oborem je množina M, která je podmnožinou R^2
Takže obrázek, který sis nakreslil, je pouze doména funkce f(x, y), nikoliv míra (objem) podprostoru, který hledáš.
Na to by sis musel kreslit v 3-rozměrném prostoru, což je ta "vrtulka", kterou jsem zmiňoval.
Kdyby chtěl spočítat prostý obsah oblasti I, stačil by ti jednoduchý integrál a počítal bys ∫(√x - -√x)dx = 2∫(√x)dx
To by byl obsah té oblasti, ale protože nad (nebo pod) tou oblastí visí křivka f(x, y) = xy, použiješ dvojný integrál a dostaneš míru trojrozměrné množiny.