Geometrická pravdepodobnosť
12 odpovědí
Na řešení potřebuješ dvojný integrál, ale protože je to úloha k zamyšlení, tak si zkus stanovit podmínky, za kterých bude trojúhelník střed obsahovat a vytvoř postup, kterým určíš, jestli jsou pomínky splněné.
Zkus něco navrhnout a uvidíme.
Malá oprava, stačí jednoduchý integrál.
Když si vyznačíme pro názornost nejlíp svislou úsečku, která je zároveň průměrem dané kružnice a budou všechny zvolené body jen buďto nalevo nebo napravo od ní, střed kružnice v trojúhelníku neleží. Když je jeden bod na opačné straně, tak ano. Speciální případ nastane, když budou dva zvolené body přesně proti sobě, tj. budou "na průměru". To bude střed kružnice procházet středem přepony pravoúhlého trojúhelníka. To, jestli bude třetí bod zvolen na jedné nebo druhé straně od dalších dvou by měla být v podstatě pravděpodobnost 50%. Nebo je to nějak jinak? Jsem už 33 let ze školy, tak prosím o shovívavost... :-)
Rozumím myšlence, ale problém nastane, když první dva body zvolím na opačných stranách, jeden nalevo a druhý napravo.
Třetí bod musí nutně ležet na jedné straně (a sousedit s předchozím bodem), což by znamenalo, že střed je v trojúhelníku vždy.
Takže potřebujeme jiný postup.
Vezmu si (pro jednoduchost) kružnici s průměrem jedna a zvolím si na ní bez jakýchkoliv preferencí bod X.
Nezávisle na X si zvolím (opět bez preferencí) bod Y.
Dále si bez preferencí a nezávisle na X a Y zvolím bod Z.
Aby střed kružnice ležel v trojúhelníku XYZ, musí Z ležet mezi body X' a Y', které jsou protilehlé k X a Y.
Můžeme se tedy ptát, jaká je pravděpodobnost, že se Z trefí mezi X' a Y'?
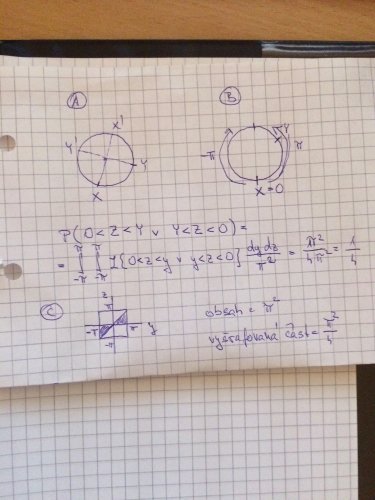
Na obrázku (A) je vidět, že vzdálenost mezi XY a mezi X'Y' je stejná, takže to bude stejné, jako bychom se ptali, že se Z trefí mezi X a Y?
Protože jsme všechny body vybírali bez preferencí, můžu jednoduše říct, že X leží v bodě 0.
A protože jsme na kružnici s průměrem 1, vybírám Y a Z na intervalu (-π, π), jak jsem vyznačil na obrázku (B).
Díky tomu dostanu formální pravděpodobnost, že XYZ obsahuje střed:
P(0 < Z < Y nebo Y < Z < 0)
To je sdružená uniformní distribuce a na její výpočet potřebujeme dvojný integrál z indikátorové funkce.
Naštěstí se dá spočítat snadno, protože odpovídá vyšrafované ploše, kde podmínky platí, jak jsem nakreslil na obrázku (C).
Výsledek je 1/4, ale asi to není nic moc k pochopení, takže ukážu trochu složitější postup, abychom si výsledek ověřili a dostali se k intuitivnímu výsledku.
Abych se vyhnul dvojným integrálům, použiju větu o úplné pravděpodobnosti:
P(0 < Z < Y nebo Y < Z < 0) podmíním tím, že Y je kladné nebo záporné.
Díky tomu si můžeme uvědomit, že je stejná šance, jestli je Y kladné a 0 < Z < Y nebo jestli je Y záporné a Y < Z < 0.
Místo původní pravděpodobnost můžu tedy počítat podmíněnou pravděpodobnost:
P(0 < Z < Y | Y > 0) a dostanu stejný výsledek.
Nevýhoda je, že opět musím použít větu o úplné pravděpodobnosti a vyintegrovat Y.
Výsledek je zase 1/4 a díky myšlence, že je jedno, na které straně volíme Y, se konečně dostávám k intuitivnímu výsledku.
To nejlepší nakonec, zvolil jsem si X, Y a Z.
X jsem položil do 0, a Y volím na pravé straně, na intervalu (0, π).
A teď myšlenka za milion.
Zvolím si Y a ptám se, jaká je pravděpodobnost, že Z bude menší?
Jenže si úplně stejně můžu zvolit nejdřív Z a ptát se, jaká je pravděpodobnost, že Y bude větší?
Protože si Y a Z volíme nezávisle, musí platit, že pravděpodobnosti, že Y < Z nebo Z > Y nebo Y > Z nebo Z < Y jsou stejné!
Obě písmenka můžu vyměnit a musím dostávat stejný výsledek, tomu se říká koherence.
Takže když volím Y a Z napravo od X, musí být pravděpodobnost P(0 < Y < Z) = 1/2
Ale protože Y si volíme napravo a Z volíme na celé kružnici, stačí mezivýsledek vydělit 2 a opět dostaneme 1/4 bez zbytečných integrálů.
Tenhle intuitivní postup má základ ve větě o symetrii rovnoměrných náhodných proměnných, která říká, že když si nezávisle na sobě volím dvě čísla A a B, tak P(A < B) = P(A > B) = 1/2
Re Tomáš: Je tedy opravdu jen 25%-ní pravděpodobnost, že střed kružnice bude ležet v trojúhelníku? Podle té Vaší úvahy bych spíš myslel, že pravděpodobnost bude čtvrtinová, že střed kružnice bude ležet mimo trojúhelník, příp., že střed bude uvnitř trojúhelníka (nebude se dotýkat jen okraje).
Když za situace, že dva body jsou proti sobě, je střed kružnice v trojúhelníku obsažen vždy, měla by se pravděpodobnost spíš zvýšit, od toho mého prvního laického úsudku 50%. Rád bych pochopil, kde v něm teď dělám chybu. Díky moc za vysvětlení.
Protože jsme na reálných číslech, je nulová pravděpodobnost, že by střed ležel na hraně trojúhelníku XYZ.
To znamená, že je jedno, jestli počítám, že střed leží uvnitř trojúhelníku bez "okrajů" nebo včetně "okrajů".
Formálně, vyberu si na kružnici dva body X a Y (nezávisle a bez preferencí), pak pravděpodobnost, že vyberu stejný bod, je nulová, P(X = Y) = 0.
No, je to pro SŠ bomba. Přitom, příklad vypadá dost nenápadně! :)
Souhlasím, ale protože je úloha "Na zamyšlení", tak je podle mě cílem stanovit podmínky, za kterých bude trojúhelník střed obsahovat a dojít k závěru, že ona pravděpodobnost je stejná jako šance, se kterou se třetím bodem trefím mezi první dva.
Samotné řešení se už bez integrálů spočítat nedá, dá se pouze odhadnout, což skoro vždycky vyjde špatně.
Vôbec nechápem, keďže integrály sú až na výške, ale ďakujem za odpoveď :D