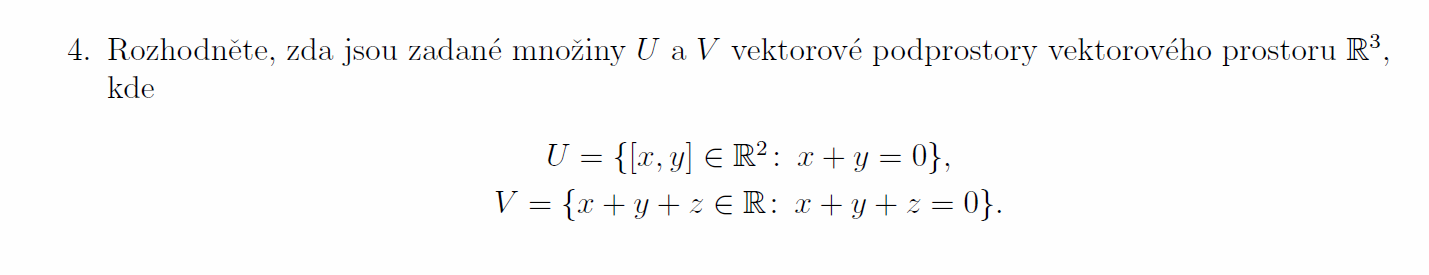Vektorové podprostory

Můj výpočet:

Ahoj Tomáši,

standardně ověřuješ uzavřenost tý množiny na sčítání a násobení konstantou. Nejsem si úplně jistej, jetstli to co tam píšeš, je úplně správně. Musel bys asi víc objasnit so tam tím myslíš, ale v zásadě stačí ověřit že součet libovolných dvou prvku je pořád prvkem U. a to samé s násobením konstantou. plus potřebuješ mít nulový prvek, což máš a potřebuješ opačný prvek ke každém, což taky máš. Takže ta jednička je v pohodě.

Co se týče tý dvojky, nerozumím úplně zadání. Co jsou konkrétně prvky tý množiny. Takhle jak je to napsaný mi to moc nedává smysl...

Přesně to jsem právě potřeboval tu dvojku objasnit, protože já tomu právě taky nerozumím - vždy jsme měli příklady typu toho prvního. Ale jinak vím, že vektorový prostor má asi 7 vlastnosti, 2 pro samotný prostor a zbytek pro operace v tom daném prostoru, tím pádem se zaměřuji jen na uzavření na sčítání a násobení konstantou. Zkusím se ještě zeptat učitele, jak to bylo myšleno (ten druhý příklad) - možná se jen upsal.

Zkus to, protože ta dvojka vypadá, jako že by to měly být pouze čísla. Teda jako jednosložkovej vektor. a ještě k tomu by ta složka měla být nulová. Je to divný....

Ahoj kluci, až tak divné to být nemusí, pokud zadání dvojky zní, že mám 3 čísla z tělesa T, jejichž součet musí být v R.

Takhle nevědomky pracujete třeba když řešíte kvadratické rovnice, máte dvě ne-reálná čísla, která po kvadratické transformaci dávají číslo reálné.

Zkuste se zamyslet třeba nad tím, co se stane, když x=1, y=-1-i, z=i.

Tahoj Tomáši, takže myslíš, že to jak je to zadaný znamená, že to je množina trojic nějakých čísel (klidně i komplexních) která vždy dohromady dávají nulu?

Ahoj Marku, klidně to můžou být i kvaterniony :-)

I když je potřeba získat intuitivní vhled, zadání musíme chápat a v důkazu postupovat čistě formálně.

Myšlenka je v tom, že omezující podmínka F(x,y)∈R je mnohem slabší než x,y∈R.

Ono to možná není tak úplně jasné, takže to pro jistotu vysvětlím hodně polopaticky.

Množina U je zadaná konstrukcí F: x,y->[x,y]∈R^2.

To znamená, že zápis [x, y] není číslo, ale konstruktor čísla (v tomhle případě vektoru R^2) - je to zobrazení.

Dokonce bychom mohli ukázat, že [x, y] je bijekce, a proto si můžeme dovolit tenhle zápis chápat intuitivně jako "číslo".

Stejně tak je množina V zadaná konstrukcí F: x,y,z->x+y+z∈R, kde F je zobrazení z T^3->R.

Co to znamená? Že V = range(F), tedy obor hodnot F, což obecně může a nemusí být vektorový prostor.

Nicméně myšlenka je identická s předchozím odstavcem.

V případě množiny V je navíc jasné, že obsahuje jediný prvek.

Když u toho příkladu upustíme od intuice a budeme pracovat tak, jak jsem uvedl výše, jedná se jenom o aplikaci pár vět na jasně definovaných strukturách, a pak na tom není nic divného.

Dokone i kdyby tam byl překlep, pořád je to platné zadání, které lze snadno vyřešit.

Jinak Tomášův důkaz pro U je korektní a líbil se mi, ale měl by tam ještě uvádět axiomy, podle kterých dělá úpravy v důkazu, aby to bylo košér.

No, to jsem právě měl na mysli tím, že je to divný. Prostě mi přišlo divný, že by V obsahovala jen jeden prvek a dělalo se kolem toho tolik cavyků :-).

No to snad ani ne :-)

Půjdu o krok dál a napíšu ekvivalentní definici pro V:

F(x,y,z) = [1 1 1]' * [x y z], F: T^3 -> R

V = image(kernel(F))

A vědět, že G=(image o kernel) vytváří podprostor (i když triviální), to už je docela užitečné, ne?