Vázaný extrém funkce o 2 proměnných

Ahoj Danieli, taky mi to nevyšlo a ono je občas dobré se trochu zamyslet, jestli ten příklad vůbec dává smysl?

Máme: f(x,y) = 80x/(5+x) + 40y(10+y) - 2x - 2y

Omezující podmínka: x + y = 25000

Takže můžu udělat malou akrobacii:

f(x,y) = 80x/(5+x) + 40y(10+y) - 2x - 2y = 80x/(5+x) + 40y(10+y) - 50000 < 80 + 40 - 50000 = -49880

Takže zisk firmy nikdy nemůže být v plusu a nejvýhodnější je nedávat žádné peníze a zůstat na nule.

Taky se můžu zamyslet trochu víc a všimnout si, že je otázka, jak rozdělit 25 tisíc, ne 25000.

Nová omezující podmínka tedy bude: x + y = 25

Substitucí dostanu:

y = g(x) = 25 - x

f(x, g(x)) = 80x(5+x) + 40(25-x)/(35-x) - 50

A teď už stačí jen postavit derivaci rovnou nule:

df/dx = 400/(5+x)^2 - 400/(35 - x)^2 = 0

Teď už opravdu vyjde 15 a 10 tisíc, ale ne 15000 a 10000.

Ahoj Tomáši, mnohokrát děkuji za pomoc! Druhý výpočet je samozřejmě správný. Ukázalo se, že jsem vazební podmínku špatně dosadil do předpisu funkce f.

Také mě napadlo, že když si nakreslím funkci g(x)= 25-x do grafu, tak je to klesající lineární funkce s průsečíky Py=[0,25] a Px=[25,0]. No a když chci rozdělit 25 tisíc do reklamy mezi TV a rozhlas, tak se nebudu pohybovat na celé přímce, ale pouze na části pro x náleží <0,25>, protože nemůžu někam dát např. 26 tísíc a jinam -1 tisíc.

Tak jsem si říkal,že pro tu funkci hledám extrémy na celé přímce a právě proto je to špatně. Ale to je asi špatná úvaha, protože vzhledem k zadaní funkci mi tedy extrém jinde než na úseku x náleží <0,25> vyjít nemůže pokud se nemýlím.

Danieli, uvažuješ správně a je neštěstí našeho školství, že musíš počítat příklad, aniž bys mu rozuměl.

Vysvětlím ti to, abys pochopil, že jsi uvažoval správným směrem.

Podívej se na ten příklad jako majitel firmy.

Analytické oddělení ti dodalo finanční model výnosu firmy v závislosti na reklamě:

f(x,y) = 80x/(5+x) + 40y(10+y) - 2x - 2y

za podmínky, že: x + y + 25

Takové funkci se také říká zisková funkce.

Pokud se budeš v budoucnu zabývat optimalizací, tak zisková funkce se maximalizuje, ale většinou se pracuje se ztrátovou funkcí, kterou naopak minimalizujeme.

Tuhle funkci můžeme rozdělit na dvě části (to je nesprávný krok, ale užitečný pro pochopení):

televize(x) = 80x/(5+x) - 2x

rozhlas(y) = 40y(10+y) - 2y

Všimni si, že investice do televize říká, že vkladem x jsi ve ztrátě 2x, ale zisk je až 80-násobný.

Ovšem někdy se reklama mine účinkem a její efektivita je daná procentem, x/(x+5).

Pro kladné x je x/(x+5) větší než nula menší než jedna - to jsou procenta.

Jinými slovy za každou tisícovku do televizní reklamy automaticky tratíš dva tisíce, ale můžeš vydělat až 80 tisíc podle efektivity.

Proč to tak je?

Ztráta je dvakrát vyšší, například proto, že místo reklamy jsi mohl za tu tisícovku udělat výrobek a prodat ho.

Efektivita v procentech zase zohledňuje podíl trhu, který jsi schopen oslovít.

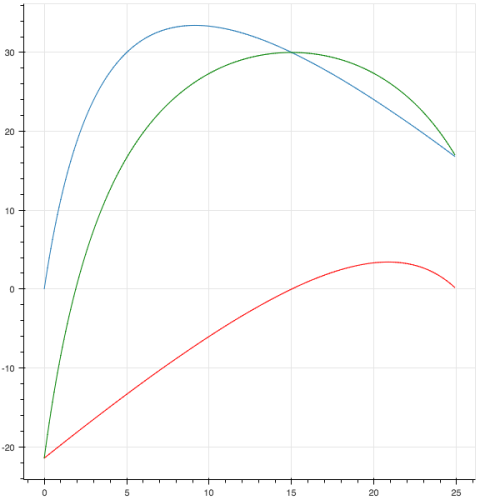
Do přílohy jsem připojil obrázek.

Modrý graf je televize podle investice 0-25 tisíc.

Červený graf je rozhlas podle investice 25-0 tisíc (tady jsem otočil osu, aby televize+rozhlas=25).

Zelený graf je jejich součet, původní funkce f(x,y), u které hledáme maximum.

A to maximum je vidět poblíž x=15.

Podle zadání hledáš maximum na množině g: x+y=25, další podmínky jsou x,y >= 0.

Tady už maximum znáš, x=15, y=10.

Jenže se podívej pořádně na graf, maximum televize je okolo x=9 a rozhlas je pro y >= 10 už jen ztrátový.

Globální maximum funkce f(x, y) tedy bude někde jinde.

K tomu stačí spočítat parciální derivace a zjistíš, že maxima nabývá na f(x=9.14, y=4.14).

To vypadá jako poloviční investice do reklamy s vyšším ziskem o 20%.

Bohužel, je to naprosto chybná úvaha, ale vysvětlit důvody, proč to tak je, je o dost složitější a spadá do statistiky.

V tuhle chvíli musí stačit, že podmínka x+y=25 nesmí být porušena.

Tím pádem hledáme extrém na celé množině x+y=25.

To je v prvním kroku daleko jednodušší a nerovnosti necháme stranou, tím se zabývá až lineární programování.

Pokud maximum v prvním kroku najdeme pro x<0 nebo y<0, otestujeme jenom hraniční body, f(0, 25) a f(25, 0) a vyšší hodnota bude globální maximum na zadané množině.

Tady jsme měli štěstí, a protože x=15, y=10, nemusíme se krajními body vůbec zabývat.

Když řešíš podobné příklady, měly by na tebe funkce takhle mluvit a vysvětlovat ti, co vlastně počítáš.

Život je pak daleko jednodušší, což jsi zjistil svojí vlastní úvahou, že nemůžeš investovat -1 tisíc, nebo že jsou výsledky nesmyslně velké.

Tomáši skvěle a srozumitelně vysvětleno. Vzhledem k mé prozatimní úrovni matematiky a specializaci není již třeba více dodávat. Je dobré vědět, když počítám nějaký příklad, co je za tím počítáním. Protože bez správného pochopení příkladu se nejedná o nic jiného, než o relativně jednoduché počítání.

Jde o to, že studuju pedák a tam se optimalizací či něčím podobným asi zabývat nebudu, i když třeba na to později dojde. Nicméně mi připadá zbytečné počítat takovéto aplikační úlohy, když nám nebyl vysvětlen tento typ úloh. Je sice supe super že na to umím uplatnit postupy, ale na to by určitě stačil normální typ úloh se zadanou funkcí, vazební podmínkou a nic jiného. To co se nenaučim ve škole se snažím dohnat samostudiem, ale je to těžší. Tak děkuji za menší přednášku, hodně mi to pomohlo :-)