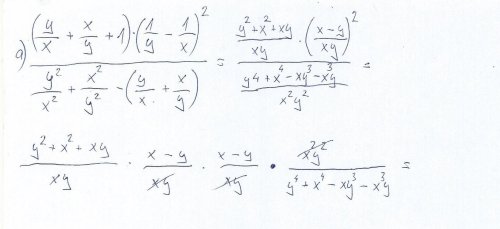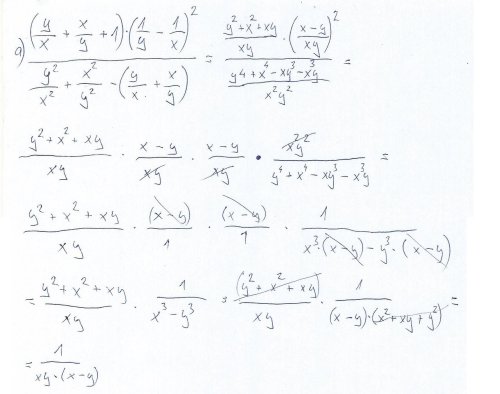Zjednodušení výrazu - složitý složený zlomek
Dobrý den, pomohl by mi prosím někdo s výpočtem tohoto příkladu? Nějak jsem to zjednodušoval, ale nějak se mi to nezdá, příjde mi, že jsem nepostupoval správně. Nemám k dispozici výsledek, z jehož pomocí bych výpočet pořád opakoval, až bych došel ke správné odpovědi. Díky předem
František N.
15. 02. 2015 16:26
6 odpovědí
Dobrý den, osobně bych sečetl všechny zlomky pomocí společných jmenovatelů a poté bych násobil tři zlomky, kde se většina krásně zkrátí. Mně to vyšlo 1/(xy) a podmínky: x nerovno 0, y nerovno 0 a x nerovno y. Je zde třeba znát vzorec a^3-b^3. Také bych zbytečně neroznásoboval, nechat v součinu, aby se dalo krátit. Pokud to nepůjde, můžu Vám poslat stručný postup.
Doufám, že to pomohlo :-)
Martin
Děkuji, já jsem to zkoušel znovu ale zaseknu se a nevím jak dál. V tom mém výpočtu jsem dál nepokračoval, protože už si teď myslím, že jsem něco udělal špatně
Omlovám, zapomněl jsem to tam napsat, je to asi nejtěžší část příkladu. Ten jmenovatel v posledním zlomku je třeba rozdložit na součin pomoci POSTUPNÉHO VYTÝKÁNÍ a až poté požijete ten vzorec, který se tam objeví. Vytkněte z x^4 a -x^3y x^3 a z y^4 a -xy^3 -y^3 - poté je to už celkem jasné :-)
Martin
Děkuji, určitě mi to hodně pomohlo, ale výsledek mám jiný než vy. Nevíte, kde jsem udělal chybu?
Je to taková klasická chyba, která se stane každému alespon jednou v životě :-) V prostředním řádku krátíte (x-y)(x-y), ale krátit lze pouze ve tvaru součinu. Jak jsem psal výše, prvně jste vytkl správně, ale je třeba vytknou dále dvojčlen (x-y), proto se to jmenuje postupné vytýkání :-) Pak tam tedy zbyde (x-y)(x^3-y^3), povšimněte si, že (x-y) je tady pouze jednou. Prostě je třeba dbát pravidla, že krátit pouze ve tvaru součinu. Opticky by člověk už chtěl krátit, ale prostě se to tak dělat nesmí :-)
Martin
Děkuji moc