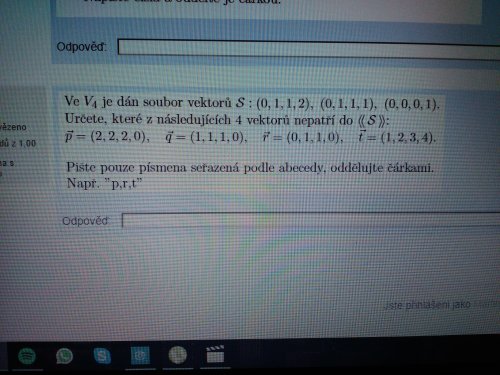
Úloha, soubor vektorů

Ahoj Martino, v příkladu musíš zjistit, které z vektorů patří do lineárního obalu S.

Protože lineární obal nad tělesem T tvoří vektorový podprostor, stačí zjistit, jestli zadané vektory patří do <<S>>.

Jinými slovy, pokud můžeš vektor p vyjádřit jako lineární kombinaci vektorů S, patří p do <<S>>.

V obecném případě bys musela řešit soustavu rovnic, ale tady je řešení vidět ihned.

Počkat počkat, to je na mě moc odborné nerozumím tomu :D Takže stačí si ten soubor vektorů zapsat do matice, přidat k tomu vektor p, a zjistit tak, jestli to patří do <<S>>?

Tak tomu zase nerozumím já, matice je číslo, ne forma zápisu.

Tobě stačí, když ukážeš, že se vektor p (ne)dá zapsat jako linární kombinace vektorů S:

p = a(0, 1, 1, 2) + b(0, 1, 1, 1) + c(0, 0, 0, 1)

Pokud dokážeš najít (nenulové) hodnoty a,b,c tak, abys splnila tuhle rovnost, musí p patřit do <<S>>.

Já tomu stále nerozumím vůbec :D

Marek tu má kurz na lineární algebru http://mathematicator.com/index.php?page=kurzy&a=6

Tohle jsou, bohužel, základy, bez kterých to nejde.

Zkus si v učebnici načíst, co je to lineární kombinace a jak se počítá, nic víc k tomu nepotřebuješ.

Ahoj Martino,

v podstatě potřebuješ vyjádřit vektor p, q, r, a t, jako lineární kombinaci těch vektorů ze souboru S.

To se dá udělat několika způsoby a jeden z nich je, že ty vektory z S napíšeš do matice po sloupcích, ten vektor p dáš na pravou stranu a řešíš soustavu rovnic. Pokud má řešení, tak je ten vektor p z obalu S. Je to srozumitelné?

Už to chápu, děkuji moc! :)

Good :-)