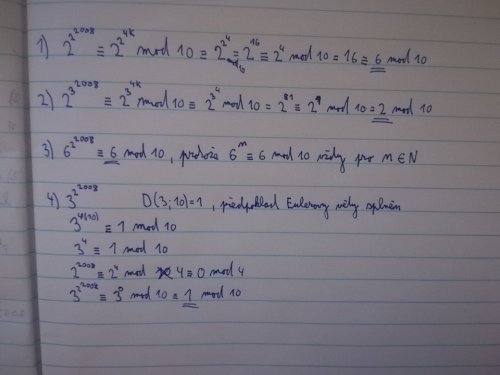Poslední cifra velkého čísla
Dobrý den, potřeboval bych poradit, už jsem fakt zoufalý :-)
Jakým způsobem se budou řešit následující problémy?
Ukol č. 3 je jednoduchý, protože 6 na cokoliv tak na místě jedniček bude vždy 6.
Umím vyřešit typ např. ''2na2008'' tak stačí exponent vydělit 4 a podle zbytku určím poslední cifru, protože při násobku 2 můžeme mít cifry 2,4,8,6.
Ale nevím si rady když mám něco na exponent a to ještě na exponent ( v tomto případě nemůžeme využít pravidel pro počítání s mocninami).
Byl bych moc rád, kdyby mi někdo objasnil situaci.
Daniel K.
13. 12. 2017 00:11
4 odpovědi
Ahoj Danieli, uděláš úplně to samé, jenom pracuješ s exponentem.
3^(2^2008) - jaký je zbytek po dělení 10?
protože 3^4 = 81 a zbytek je 1, stačí pro 2^2008 najít zbytek po dělení 4 a umocnit 3 na zbytek
2^(3^2008) - jaký je zbytek po dělení 10?
protože 2^4 = 16 a zbytek je 6, stačí pro 3^2008 najít zbytek po dělení 4, umocnit 2 a vynásobit 6
Když navíc budeš trochu přemýšlet, tak příklad (3) víš z hlavy, pak spočítáš (4) a hned uhádneš (1).
Ahoj Tomáši, děkuji moc za odpověď, pomohl jsi jako už několikrát.
Chvíli mi trvalo, proč u toho druhého příkladu ještě násobíš 6, když u toho čtvrtého jsi to nenásobil, ale tam je vlastně zbytek 1 takže násobíš 1.
Ještě jenom pro kontrolu nebo pro ostatní sem dám mé řešení pomocí kongruencí.
Měl jsi říct, že víš, co je to kongruence a Eulerova věta, to bych to nemusel vysvětlovat tak složitě :-)
Tvým postupem si nejsem uplně jistý, zdá se mi, že jsi přeskočil nějaké úvahy, které jsou k důkazu potřeba.
Příklad #1
2^(2^2008) mod 10 ≡ 2^(4p+q) ≡ (2^4)^p * 2^q ≡ 6^p * 2^q ≡ 6 * 2^q
protože 4 | 2^2008 => 2^(2^2008) mod 10 ≡ 2^(4p+0) ≡ 6
Mám o tom nějaké představy, umím to snad i správně využívat, akorát správný zápis, aby to bylo všechno matematicky korektní mi dělá problém.
Opsal jsem si to a už je mi to jasný, takže děkuji. :-)