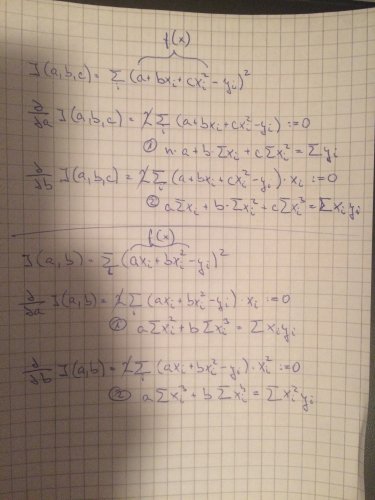Metoda nejmenších čtverců
Ahoj! Pomocí metody nejmenších čtverců mám proložit polynomem ax+bx^2 určené hodnoty. Mohu použít pro výpočet vzorec pro parabolu s tím, že by pomyslné c bylo rovno nule? Předem děkuji za odpověď.
Zuzana B.
29. 12. 2017 22:30
4 odpovědi
Ahoj Zuzano, jak chceš použít vzorec pro parabolu?
Pro regresní funkci můžeš použít libovolné regresory, a to včetně konstanty "c", kterou naopak můžeš vypustit (viz "libovolný" regresor).
Na druhou stranu to ale nedává smysl, protože dostaneš vychýlený model.
Trocha statistiky: Abys mohla vypustit konstatní člen, potřebuješ hledat regresní model ve středovém tvaru, což znamená normalizovat regresory na nulový průměr, ale pokud E[x] = 0, potom E[x^2] = Var(x), který bude nenulový - a nulový bude pouze v případě konstatních dat, kde zase nemá smysl hledat regresní model.
Pro polynomiální regresi druhého stupně si prostě vezmi body (x, y) a vygeneruj nové body (x^2, x, 1, y).
Přes normálové rovnice spočítáš váhy jako u obyčejné lineární regrese a to je celé.
A jestli je to nějaký úkol na odvození vzorce, tak si sestav chybovou funkci nebo věrohodnost (podle toho, jestli je to lineární algebra nebo statistika :) jako sumu kvadrátů, derivuj ji podle jednotlivých vah a řeš pro rovno nule.
Tvoje otázka mi ale přijde nějak zamotaná, pochopila jsi dobře zadání?
Ano, zřejmě jsem nepochopila zadání. Počítala jsem příklady na metodu nejmenších čtverců, kde jsem body prokládala přímkou a parabolou podle daných vzorců. Ovšem u ax+bx^2 přemýšlela jaký vzorec použít. Za a,b jsem si dosadila konkrétní čísla a graf mi vždy vyšla parabola, tak jsem zkusila použít vzorec pro parabolu a vycházela mi "nepěkná čísla". Teď s tím příkladem nemohu hnout, tak jsem se obrátila jsem. Nejspíš to bude má matematická neznalost. Připojuji příklad (pro lepší orientaci).
Už to chápu, pochopila jsi to správně, ale ten příklad je úplně pitomý :-)
Podívej se do přílohy, v horní části odvozuju metodu nejmenších čtverců - to, čemu ty říkáš "vzorec pro parabolu".
Udělám si funkci více proměnných J(a, b, c) pro polynom druhého stupně.
J(a, b, c) je suma čtverců chyb (SSE) a hledám její minimum.
Spočítám si parciální derivace podle a, b, c a postavím derivace rovny nule, z toho vyjde soustava tří rovnic o třech neznámých.
Rovnice označené (1) a (2) se shodují s tvým "vzorcem", třetí rovnici jsem neodvozoval, protože je to stejné.
V dolní části počítám to samé, ale tentokrát pro funkci ax + bx^2.
Suma je tentokrát J(a, b) a stejným způsobem dostanu jinou soustavu rovnic, kterou můžeš aplikovat na svůj příklad.
Prostě si přepiš rovnice (1) a (2) z dolní části do soustavy rovnic.
A když to porovnáš se svým vzorcem, tak si můžeš všimnout, že když ze své soustavy vyhodíš první řádek A první sloupec, dostaneš to, co jsem odvodil (a taky jsou jinak pojmenované proměnné, tak abys nepopletla původní "a" a nové "a").
Tomáši, děkuji velmi za vysvětlení a za pohotové odpovědi. :) už mi to secvaklo