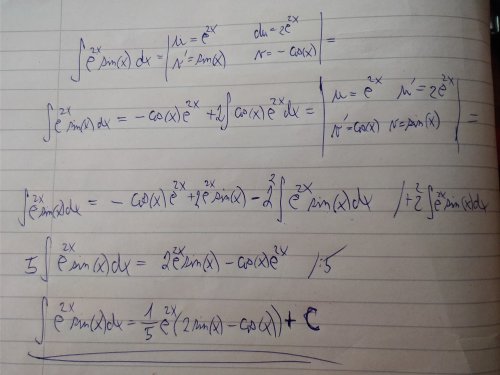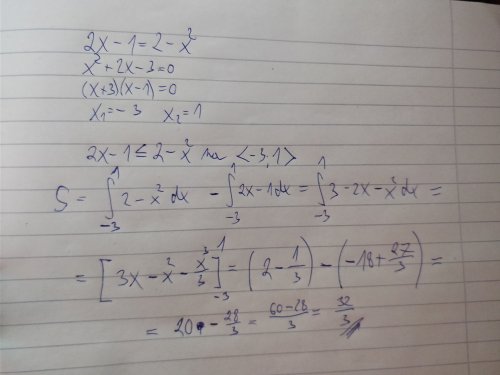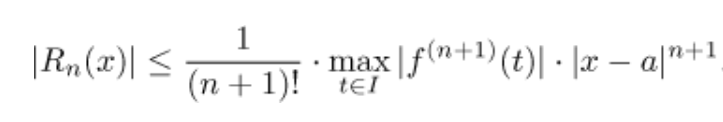Integrální počet

Tak i ty křivky neumím :-(

Ahoj,

ten první integrál se dá řešit například metodou per partes. Kdy ji budeš muset použít vhodně dvakrát. Může se člověk do toho docela jednoduše zamotat - hezky se tam vytváří jakýsi cyklus. Přikládám i řešení tohoto integrálu.

U druhého příkladu jde o to najít průsečíky těch dvou křivek a zjistit, která z nich má na intervalu mezi průsečíky vyšší hodnotu. Je dobré si to nakreslit, tím člověk nikdy nic nezkazí. Pak už je myslím vše jasné.

Děkuji moc, strašně moc mě to pomohlo, strávila sem nad tím několik hodin a už asi vím jak na to :-)) Mám ještě pár příkladů můžu otravovat? Moc jich není, ale na pár sem se zasekla.

Jasně, rád pomůžu. :-)

Není jich nejmíň, ale jsou to poslední příklady, co sem nedopočítala z minulých let co byly v testu. Děkuji moc předem, vždy sem se sekla na nějaké blbosti :-(.

Míša

Tady připojuji ten obrázek :-)

Tady by nejspíš bylo dobré říct, co ti nejde, protože příkladů je hodně a na to nejspíš nebudu mít čas, ale rád poradím řešení libovolného příkladu. Taylor a průběh funkce je víceméně o spravném výpočtu derivace. Na řadu použiješ Leibnizovo kritérium a jak je ta limita posloupnosti nahoře, vybral bych z ní dvě posloupnosti a ukázal, že jejich limita není stejná.

Vím není toho nejmíň :-(, sem z toho už zoufalá :-(.

Taylorův polynom není těžký, derivace dokážu udělat a pak to i správně zapsat, ale nechápu z prezentace jak odhadnu tu chybu, zdá se mě že mám víc neznámých než rovnic.

U té limity posloupnosti zas neumím jak vybrat vhodné posloupnosti a co znamená ta závorka

Tu řadu zkusím dopočítat pomocí Leibnizova kritéria, to mě nenapadlo a to vyšetření funkce zkusím znova vypočítat a pošlu scan, třeba najdeš kde dělám chybu.

Na odhad chyby té aproximace je dobré použít tvar zbytku a trošku si s tím pohrát. :-)

Ta závorka je funkce celá část. Platí : floor(x)=n právě když n<=x<n+1 (pro n celé) , kde floor je ta celá část. To znamená, že je to jakési zaokrouhlování dolů na nejbližší celé číslo. Například floor(3,4)= 3 , floor(-3,5)= -4 atp. Pokud máš tu posloupnost a_n tedy, tak bych se třeba podíval, jak vypadá posloupnost a_(6k-3) a třeba a_(6k) (pro k celé) a zjistil bych jaké jsou limity těchto (pod)posloupností.

Ja tu limitu nechapu :(, nerada bych napsala nejakou hlupost do zk