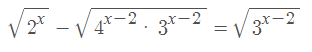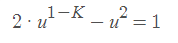Exponenciální rovnice
10 odpovědí
Ahoj Ondro, dosazením se dá přijít na to, že kořenem je dvojka, ale dojít k tomu úpravami se mi zatím taky nedaří. Ještě si s tím zkusím pohrát.
Ahoj Ondro a Marku.
Tahle rovnice mi přišla hrozně zajímavá a strávil jsem nad ní taky docela dost času. Až už jsem si prostě nevěděl rady, tak jsem googlil. Takže tohle řešení není moje, ale je to tak zajímavý, že se musím podělit.
Edit: Koukám, že ten konec není moc vidět, přidám tedy ještě jednu fotku.
Edit2: Dá se ještě použít substituce x-2=2m. Dojde se k rovnici 2*2^m - 12^m = 3^m, která má řešení m=0 => x-2=0 => x=2.
Ahoj, pokud bude u=1 tak potom ta rovnice je 21^(1-k)-1²=1 21-1=1 2-1=1 1=1
Jedna na cokoliv je jedna. Pokud teda nepočítáme limitu a nějaký nekonečna.
No to ano, ale jestli jde k tomu výsledku dojít i pomocí ekvivalentních a neekvivalentních úprav. To samé je jako zadání, na druhý pohled je jasné, že to vyjde x=2, a ověřit jen zkouškou.
Ještě jsem posílal to druhé řešení. Substituce x-2=2m. Každopádně u toho to taky není 100% korektní. Tam taky nevím, jak se dopočítat m=0 kromě toho, že to prostě zkusím.
Marku, Vás něco napadlo?
Ahoj Ondro, když píšeš "numericky dokázat", myslíš zřejmě "dokázat analyticky", a když píšeš "dojít k výsledku pomocí ekv. a neekv. úprav", myslíš "vydělit proměnnou x na jednu stranu rovnice".
Odpověď na první otázku je jednoduchá, rovnici lze snadno převést do tvaru 1 + 1 = e^ay + e^by, pro a,b>1.
Protože funkce na pravé straně je monotonní, existuje nejvýše jedno řešení a ihned je vidět, že řešením na R je jen a pouze nula.
Odpověď na druhou otázku je také jednoduchá, lépe to nejde.
Ne všechny rovnice mají řešení ve formě konečného analytického zápisu.
Dokonce existuje i typ čísel, který nelze vyjádřit ve formě rovnice s konečným počtem operací.
A pokud by koeficienty rovnice nebyly pečlivě zvolené, výsledkem by ihned bylo takové číslo.
Ahoj, ano to jsem si popletl dva pojmy numericky/analyticky.
Jinak děkuji za odpovědi a ujasnění...