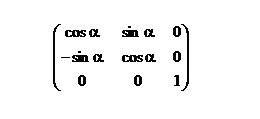Transformační matice
Dobrý den,
mohl bych se zeptat, jak to je s transformační maticí? Například rotace kolem osy z?
Jak se tvoří vlastně takové matice?
Proč tam je v té rotaci třetí řádek 0 0 1 a třetí sloupek 0 0 1? Děkuji za odpověď. :)
Jiří H.
17. 08. 2018 19:45
2 odpovědi
Matice má více interpretací, z pohledu transformace je každá [regulární] matice X lineární transformací do vektorového prostoru s bází inv(X), případně do podprostoru s degenerovanou bází, pokud je X singulární.
Transformaci uděláš tak, že si nejprve vytvoříš bázi a spočítáš si její inverzi.
Například ve 2-rozměrném prostoru chci udělat otočení proti směru hodinových ručiček, což je transformace daná bází
[0 -1]
[1 0]
Její inverzní matice je potom
[0 1]
[-1 0]
Tuhle matici už můžu použít ke zmiňované transformaci.
Ve tvém případě máš matici pro rotaci okolo osy Z, což znamená, že po transformaci se souřadnice z nemá změnit.
To si můžeš ověřit vynásobením své matice libovolným vektorem; pro poslední řádek platí [0 0 1] * [x y z] = z.
Stejně tak pro poslední sloupec platí [u v 0] * [x y z] = ux + vy
Tak jedná se o rotaci kolem Z, kdyby se jednalo o rotaci kolem jiné osy, tak bude jednička na příslušném místě diagonály obklopená nulami, kdyby to ale byla obecná transformace , tak se musí skládat jednotlivé koeficienty z kombinací všech směrových cosinů a funkce sinus tam nebude figurovat vůbec, v rovině vlastně jsou směrové cosiny také dány dvěma úhly, jenže protože druhý úhel je doplňkem v rovině do pi/2, tak se místo toho uvažuje jeden úhel ,ale dvě funkce cos a sin. Jinak v obecném již v E(3) případě to budou vždy součiny směrových cosinů a v případě jednoduché rotace jako zde v E(3) se to zjednoduší pomocí vztahů v rovině, proto tam je funkce sin, a tak to může být i u jednoduchých rotací i v E(4) a dalších prostorech.