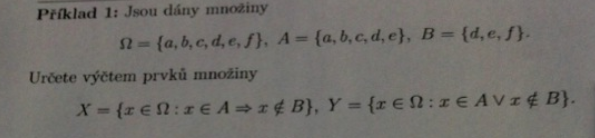Sestavení množiny
Máme dány tři množiny výčtem prvků a úkolem je vytvořit další dvě množiny X a Y, které budou splňovat podmínky uvedené pro každou množinu.
Podmínky jsou zapsány pomocí výrokové logiky.
Viz. obrázek
Nejsem si úplně jistý jestli tomu rozumím správně - zvláště pak množina X a to pravidlo pro její prvky zapsané pomocí implikace.
Rozumím tomu tak, že X má obsahovat takové prvky množiny omega, které splňují tuto podmínku: jestliže je prvek v množině A, potom nesmí být v množině B. Pokud pro libovolný prvek ze všech tří zadaných množin (omega, A, B) toto platí a tedy implikace je pravdivá, potom tento prvek dám do X. Pokud implikace pravdivá není tak do X prvek nedám.
Chápu to dobře? Díky,
Tomáš K.
19. 08. 2018 17:50
2 odpovědi
Chápeš to dobře, jen upřesním, že to nemusí být prvek ze všech tří zadaných množin, musí být nutně v množině omega, ale obecně určitě ne v A či B; např. pokud by Ω měla ještě navíc prvek g, tak ten by to X také patřil, i když není v A ani v B. Ty implikace nejsou někdy průhledné, tady lze ještě snadno uvážit, že v množině X budou prvky a,b,c; ale už ne tak čitelné je, že tam bude i prvek f. Proto je někdy vhodné si implikaci přepsat na konjukci/disjunkci, a to ze znalosti, že ¬(A => B) lze zapsat jako (A ∧¬B), ale platí ¬(C ∧ D) <=> (¬C ∨ ¬D), tedy musí nutně platit (A => B) <=> (¬A ∨ B). Podle toho lze podmínku v množině X přepsat jako: (x∉A ∨ x∉B), z toho můžeme ještě pro větší přehlednost "vytknout" negaci: ¬(x∈A ∧ x∈B), takže tam nesmí být prvky, co jsou v A i B, tedy jejich průnik, z toho plyne X = Ω ∖ (A ∩ B).
Super vysvětlení, díky