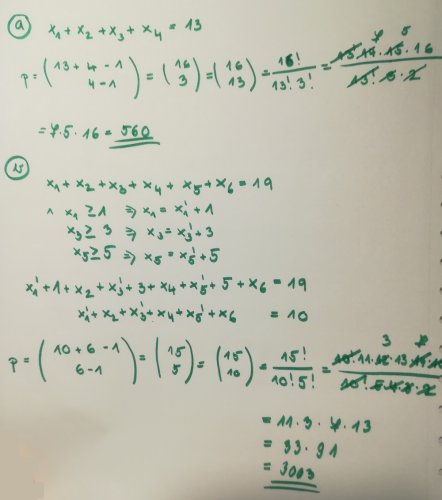Rovnica (koľko existuje riešení...)
Dobrý deň, mohol by mi niekto prosím vysvetliť, ako sa riešia príklady typu ´´Nájdite počet všetkých celočíslených riešení rovnice, ak... ´´ a rovnica je x1 + x2 + x3 + x4 = 10 a platí, že x1>=1 ?
Ďakujem.
Barborka A.
06. 01. 2019 17:14
4 odpovědi
A nechybí tam ještě podmínka, že všechna x musí být nezáporná?
Dobrý deň, áno, je to možné, nebola som si na 100% istá, keďže zadanie už nemám dostupné celé.
Nejdriv je potreba rovnici prevest do tvaru, kdy plati ze vsechna x >= 0.
To muzu udelat substituci: x1' + 1 = x1
x1 = x1' + 1 >= 1
x1' >= 0
Po dosazeni do rovnice:
x1' + 1 + x2 + x3 + x4 = 10; kazde x >= 0
x1' + x2 + x3 + x4 = 9; kazde x >= 0
Pocet reseni odpovida poctu zpusobu, kterymi muzu 9 kulicek dat do 4 prihradek, na coz je vzorecek (ktery se da snadno odvodit) a rika se mu Bose-Einstein, cesky, myslim, kombinace s opakovanim.
(9 + 4 - 1 nad 4 - 1) = (12 nad 3) = 220 reseni
Dobrý deň,
ďakujem Vám za pomoc. Prosím Vás mohli by ste sa pozrieť, či sú správne vyriešené tieto 2 podobné príklady?
Ďakujem.
