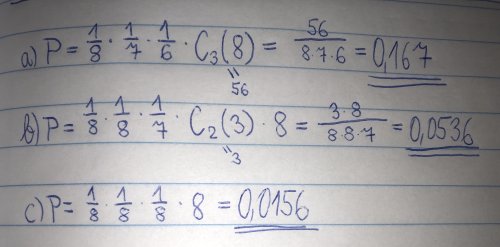Pravděpodobnost
9 odpovědí
Můžeš si udělat jednoduchou kontrolu, protože po výběru 3 číslic platí, že jsou buď rúzné, nebo se dvě shodují, nebo se shodují tři.
Tedy P(a) + P(b) + P(c) = 1, jenže tvoje výsledky dávají v součtu cca 0.24
Možností, že každá číslice bude jiná, je 8 krát 7 krát 6, to jest 336.
Možností, že dvě číslice budou stejné, je 8 krát 1 krát 7, to jest 56.
Možností, že všechny tři číslice budou stejné, je 8 krát 1 krát 1, to jest 8.
Jiné možnosti už nastat nemohou, takže počet všech možností rovná se 336 plus 56 plus 8, to jest 400.
Pravděpodobnost jevu a) 336/400 jevu b) 56/400 jevu c) 8/400
Samozřejmě, je lepší si výsledné zlomky pokrátit, popřípadě převést na desetinná čísla či procenta.
Ahoj Jarmilo, ve variantě (b) musíš započítat všechny možnosti, jak vybrat dvě stejné číslice.
Opět kontrola, všech čísel, která můžeme zkontruovat, je 8^3, nikoliv 400.
Je to jak píše Tomáš, 56 je to jen pro případ, že se shodují číslice na 1. a 2. pozici, ještě je potřeba započítat případy, kdy se číslice shodují na 1.a 3. pozici a 2.3. tedy počet možností jevu b je 56*3=168. a potom už sedí kontrolní součet.
Děkuji, hrubá moje chyba, že jsem zapomněla u béčka měnit pořadí. Člověk si myslí, že má za jedna, o ono to je za pět. Zkusím napsat nové výsledky, ale už si raději nemyslím, že to je stoprocentně dobře.
Pravděpodobnost (zaokrouhlená):
a) 0,66
b) 0,33
c) 0,01
Ještě bych byl opatrný se zaokrouhlováním, protože ppst (b) je asi 20x vyšší než ppst (c), ale podle čísel je 30x vyšší?
Zaokrouhlovat je nutné na stejný počet platných číslic, nikoliv počet desetinných míst (to je naopak špatně).
Výsledek (c) 0,016 už sedí mnohem lépe.
Ajaj, děkuji, pane Tomáši B. Bývalo by lepší, kdybych výsledky nechala ve zlomcích-