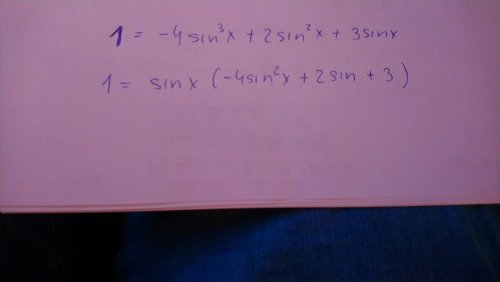Goniometrie
Dobrý den,
prosím o radu jak upravit rovnici sin3x=cos2x.
Už nad tím bádám dva dny a nemohu se dopočítat.
Monika B.
18. 04. 2019 07:24
3 odpovědi
Pavel M.
18.04.2019 07:24:57
Ahoj, úprava by měla být správná. Došel jsem ke stejné. :)
MILAN K.
20.02.2020 18:02:48
Tak jelikož platí, že cos alfa = sin (pi/2-alfa,) tak potom také platí sin 3x = cos (pi/2-3x) a jelikož bylo dáno sin 3x = cos 2x, tak potom také platí cos (pi/2-3x) = cos 2x.
Takže cos (pi/2-3x) = cos 2x, z toho plyne, že arccos (cos (pi/2-3x)) = arccos (cos (2x)) , tedy pi/2-3x = 2x. Dále z toho plyne, že pi/2 = 2x+3x = 5x. Čili pi/2 = 5x. Tedy x = pi/2 / 5 , tedy x = pi/10 = 18°. A totéž pro pi/10 + k 2pi . Čili například sin (318°) =cos (90°- 318°) = cos (218°)
Pro napsání komentáře se musíte přihlásit.