Logaritmická funkce
Dobrý den, moc se omlouvám za hloupou otázku, snažil jsem se na to přijít a nemrhat Vaším časem, ale opravdu si nevím rady.
Zatím jsem se vždy setkal s příkladem, kde x bylo v závorce, jak bych měl prosím postupovat, pokud to tak není? Jak najít průsečíky?
A jak číst posuny grafu? Myslel jsem, že hodnota -3 ( protože je mimo závorku ) je hodnota "c", která mi posouvá fuknci směrem dolů? Ale z grafu to vypadá, že nic nedělá.
Jakub V.
10. 08. 2019 11:42
4 odpovědi
Ahoj k posunům grafu:
funkce y=log x-3 je oproti funkci y=log x posunuta o 3 dolů
funkce y=log x+3 je oproti funkci y=log x posunuta o 3 nahoru
funkce y=log (x-3) je oproti funkci y=log x posunuta o 3 doprava
funkce y=log (x+3) je oproti funkci y=log x posunuta o 3 doleva
K hledání průsečíků s osami:
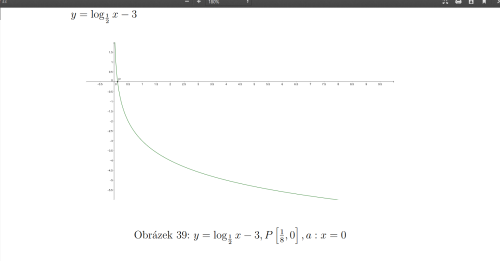
Je to stejné jako u ostatních funkcí, když hledám průsečík s osou x dosadím za y nulu 0=log1/2 x-3 3=log1/2 x
x=(1/2)^3=1/8
Tato funkce nemá s osou y průsečík, protože osa y (tj. přímka x=0) je asymptotou této funkce, takže se k ní nekonečně přibližuje, ale nikdy jí neprotne.
Asymptotu najdeme u logaritmu tak, že budeme hledat x, pro které je argument funkce (hodnota v závorce) rovna 0.
Ahoj, mockrát děkuji za odpověď! :-)
Pokud by Ti to nevadilo, mohl by si mi zkontrolovat obrázek, jestli to chápu dobře? Rozepsal jsem si to krok po kroku, abych se k tomu mohl kdyžtak vrátit.
A ještě jednou díky! Spočítal jsem si další příklady a vše hezky vychází, moc pěknej pocit. :-)
Teďka hurá na procvičování gon. funkcí, která mi pletou hlavu ještě víc! :-D
PS: špatně jsem zadal fotku, omlouvám se za potencionálně vykloubenej krk. :-D
Ahoj, výpočet máš správně, jen bych ještě na začátek napsal poznámku že to počítáš pro y=0.
Přeji hodně zdaru.
Moc Ti děkuji, přeju hezký víkend. :-)