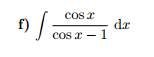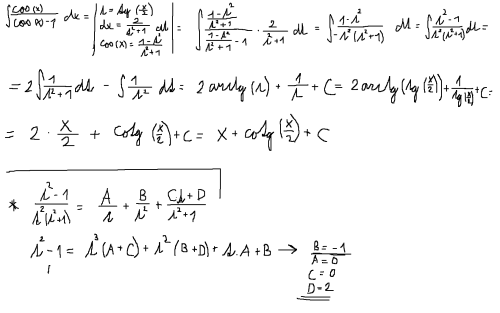Pomoc s integrálem

Až budu doma klidně ti k tomu hodím i výsledek,teď jsem ve škole,máme informatiku,tak jestli si počkáš tak hodinku,tak to tu máš. :)

Dobře díky, zkusím se s tím poprat, ale klidně mi to tady pak hoď ;-)

Tady to máš. :)

Díky, ale stejně jsem furt z toho jelen :D

No ..... mohl bys napsat přesně z jakého kroku si jelen,ať ti to můžu objasnit ?

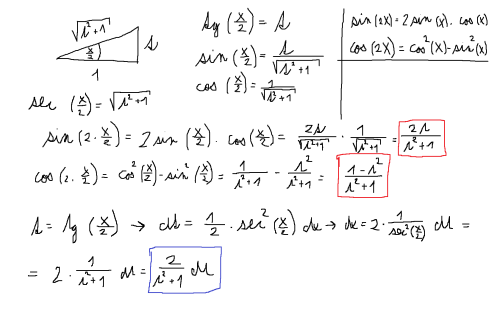
Nebo to vemu všechno od začátku .... jakmile vidíš v integrandu .... nějáký výraz ze sinama a cosinama ... prvně přemýšlíš o nějáký krásný substituci ... nebo per partes ... (třeba sin (x) . x dx) ale jakmile prostě nedokážeš přijít na žádný krásný per partes.. nebo krásnou substituci ... tak se používá substituce t=tg(x/2) .... no ... a z tohohle vztahu zjistíš .. pomocí goniometrických vzorců pro dvojnásobný úhel .. jak to mám na obrázku ... jakýmu výrazu se cos (x),sin(x) ... a dx rovná ... no ... pak tam dosadíš vše co víš .. viz. obrázek nahoře ... dosadil jsem za cos (x) to (1-t^2)/(t^2+1) a za dx 2/(t^2+1) jak nám vyšlo ... pokrátil jsem co se dalo ... pak jsem použil rozklad na parcialní zlomky.... vypadalo to : A/t + B/t^2 + (Ct+D)/(t^2+1) z toho mi vyšlo ... že A=0 ... tzn .. že výraz kde je A odpadá ... C=0 ... tzn ... že ve výrazu (Ct+D)/t^2+1) bude jen konstanta a ne proměnná t. No .. a jediné co mi zbylo je tedy B/t^2 + D/(t^2+1) víme že B=-1 a D=2 ... takže máme integrál 2/(t^2+1) ... když se koukneš,tak je to tabulkovej integrál .. vedoucí na arctg (t) no ... a nesmíš to zapomenout vynásobit to 2 .. tzn,že máš 2arctg(t) ... a teď ten druhej ... máš integrál ... -1/t^2 ... to mužeš napsat ve tvaru ... -t^-2 když to zintegruješ .. tak máš -1.(t^-1)/-1 no ... (-1).(-1)=1 .. takže ti zbylo t^-1 .. a to je 1/t ... samozřejmě k tomu přidáš konstantu. takže máš 2arctg(t) + 1/t + C ... dosadíš zpět místo t to tg(x/2) ... máš 2arctg(tg(x/2)) + 1/tg(x/2) + C ... tak .. a co víš o tg a arctg .. jsou to navzájem inverzní funkce.. tzn,že se vyruší .. a zbyde ti jen 2. x/2 ... to je x ... a to druhé .... 1/tg(x/2) ... použil jsem vzoreček tg (x).cotg(x)=1 .. když to vydělíš tg(x) .. vidíš že cotg (x)=1/tg(x) ... a to je přesně náš případ ... 1/tg(x/2)=cotg(x/2) ... proto náš výsledek vypadá x+cotg(x/2)+C

Dobrá, to už mi pomohlo...díky moc

Rádo se stalo. :) je to lehký poznat že tam bude ... když prostě nevidíš per partes ... nebo klasickou substituci ... nebo nějáký zlehčení pomocí gonio. vzorečků ... tak jednoduše t=tg(x/2) ... a už zase jedeš .. dosadíš za sin(x) .. apod ... pokrátíš ... obvykle rozložíš na parcialní zlomky .. spočteš,zintegruješ a hotovo. :)

Honzo, dneska jsem na substituci tg(x/2) natočil video a myslím, že se opravdu povedlo :-) Je jako bonus v kurzu Integrály. Takže jestli ten kurz máte, tak se na to video můžete podívat. Ta substituce tg(x/2) je taková mrcha složitá :-)

http://mathematicator.com/index.php?page=kurzy&a=2

Jinak Vladane... klobouček :-)

Parádní video...díky :-)

Super. Jsem rád, že se líbilo :-)

Ahoj,tenhle integrál se počítá takzvanou Weierstrassovo substitucí... dej si t=tg(x/2) ... z toho cos (x)= (1-t^2)/(t^2+1) dx= 2/(t^2+1) .. to tam dosaď,pokrať a je to. :) kdyby něco,tak mi ještě napiš. :)