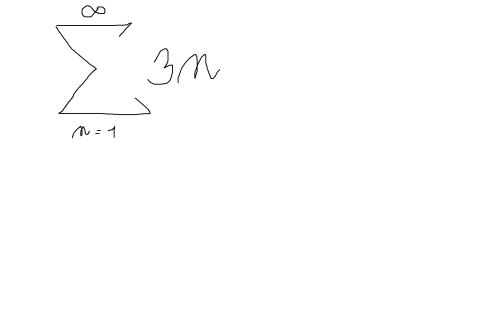Nekonečné řady

Ahoj (-1)^n .. není nekonečná řada ... co by na ní bylo nekonečného ... pro n=3 je -1 ... n=4 je 1 ... ale nepočítáš s nekonečnem.... zato suma pro n=1 do nekonečna je nekonečná řada.. ale vždy tam musíš mít nějákej výraz... jinak to nedává smysl.

Tohle je například nekonečná řada.

Ej... pardon ... blbě jsem to přečetl .. to jestliže je to suma n=1 do nekonečna z (-1)^n tak je to nekonečná řada .... promiň.

Děkuji a co zápis (1/n) pro n=1 až do nekonečna

není tam suma, jen tento výraz

Ahoj,s tímhle se moc nepotkáš... obvykle to je zapsané sumou,ale jestli tě chápu dobře,tak ano.Ani nevím,jestli takový zápis existuje..(Používám jen zápis sumou),ale jestli ano,tak by to byla nekonečná řada taky.

Pánové bacha ! Ta otázka je jiné kategorie než si myslíte.

Jedná se o rozdíl mezi nekonečnou posloupností a nekonečnou řadou. Posloupnost je nějaká uspořádaná množina prvků, třeba čísel. Například 1,2,3,4,5,6,7,8....

Pokud to pokračuje až do nekonečna, je to nekonečná posloupnost. naky se to může zapisovat jinýmy způsoby. Například { an} n=1 až nekonečno an=n+2. to je posloupnost 3,4,5,6,7,8,9,....atd až do nekonečna.

A teď ta pointa: ŘADA to je, když ty členy té posloupnosti budeme sčítat. Tedy například 1+2+3+4+5+6....

A jeden ze způsobů jak to zapsat je práve pomocí sumy. To, jestli ta řada je nebo není nekonečná, je otázka akorát toho, jestli sčítáme konečný nebo nekonečný počet členů. Ale to hlavní je, jestli je to ŘADA jako taková. A aby to mohla být řada, musí se ty jednostlivé členy sčítat.

Já vím co je řada a poslupnost.Však ... kde jsem řekl něco špatně ? jestliže je to suma (-1)^n od n=1 do nekonečna ... tak je to nekonečná řada ... která vypadá : -1+1-1+1-1 ... No .. a pod zápisem ... 1/n pro n=1 až do nekonečna jsem si možná špatně představil .. součet 1+1/2+1/3+1/4 ... jestli to byl vzorec pro výpočet n-tého členu poslupnosti,tak se omlouvám.

No, já právě myslím, že to je přesně tak. oni dávají takovýhle chytáky do testů. Zorvna to řeším s jedním svým studentem. Napíšou zakroužkujte co je řada. A pak tam dají posloupnost. A jde jenom o to rozlišovat mezi posloupností a řadou. a když tam není suma, nebo není naznačeno že se ty členy sčítaj, tak to není řada, ale posloupnost.

Jinak Vladane, to nebyl nějakej výpad proti tobě. Vůbec. Chtěl jsem jenom aby v tom měl Jindra úplně jasno. Z toho jak odpovídáš na fóru bych řekl že umíš matiku mnohem líp než já. Co studuješ?

Marku,Vysoká škola mě čeká až za několik let.Účím se tuhle "vyšší" Matematiku od 7. třídy základní školy ... protože mě to baví... je to můj koníček... takže trávím třeba 3 hodinky svého volnýho času učením se matematiky.Začlo to středoškolskou (protože bych se nehnul bez těch znalostí ...) a teď jsem u učiv jako : Tenzory,Plošný integrály .. apod.Jakmile tě to baví ... tak ti všechno příjde jednodušší.Každopádně ... děkuju za tu lichotku,ani nevíš jak mi to zpříjemnilo den. :) Omlouvám se,jestli to vypadalo,že jsem vyjel .. jak si to čtu,tak bys to tak mohl pochopit.Vůbec to tak nebylo myšlený.A klobouk dolů před tím co děláš . myslím,že tím pomáháš spoustě lidem! Dokážeš věci skvěle podat,to se jen tak nevidí. :)

Ještě bych doplnil co se týče těch řad ... tak jak máš aritmetickou poslupnost ... a geometrickou .. tak jakmile máš součet prvků arit. poslupnosti ... tak se ta řada nazývá aritmetická ... a když geo. poslupnosti,tak geometrická ... ale to je jen tak pro zajímavost..mimo. :)

Vladane, tak to klobouk dolů. Myslel jsem, že studuješ třeba matfyz, nebo tak. Protože třeba ta tvoje odpověď na ten dotaz s integrálem byla super. Tu redukční formuli či co to bylo...o tom jsem nikdy neslyšel :-)

Jinak, určitě to nevypadalo že jsi vyjel. Naopak, já když jsem pak četl svůj příspěvek, tak jsem si říkal, jestli jsem se nedotkl já tebe. Proto jsem to dovysvětloval. Každopádně jsem moc rád, že jsi tu a že se takhle aktivně účastníš fóra. Díky.

Marku ... ta redukční formule ... Moc se to zas tak nepoužívá .. alespoň ne teda já .. vždycky ten integrál jde spočíst něják elegantněji ... než skrz tenhle vzorec ... jsou poměrně velký .. a kdybych si to měl pamatovat pro každou funkci .. tak bych z toho zešílel.. proto mám rád matematiku .. je důležitý věci pochopit .. a ne se to drtit do hlavy jak třeba ... nějáký humanitní vědy,když si to vyhledáš na wikině ... tak sám vidíš kolik jich tam... používám to jen když vidím třeba integral cos^10(x) dx .. apoď,když je exponent hodně vysokej.. protože když bych měl použít vzorec cos^2(x)=(1+cos(2x))/2 .. tak bych se z toho zbláznil kolikrát bych to měl použít .. a k tomu umocnit.Sám si pamatuju jen pro cos^n(x) a sin^n(x) .. ostatní když potřebuju se lehko odvodí.Jinak .. Děkuju za pochvalu .moc si jí vážím! To já ti děkuju.Vůbec... že si Mathematicator vytvořil .. a že se takhle o něj staráte s Honzou.

Děkuji za inormace. Mám ještě dotaz. Mám určit, zda je splněna podmínka konvergence pro dvě rúzné řady. Jedná se o řadu suma 6 pro n=1 až do plus nekonečno a druhá řada suma j pro j=1 až do plus nekonečna?

Jindro ... stačí se na to mrknout ... máš sumu 6 pro n=1 do nekonečna .. tzn. že to bude součet 6+6+6+6+ ... a takhle do nekonečna .... takováhle řada nemůže nikdy konvergovat .... jakmile lim x-->nek (6) je různa od 0,tak řada automaticky diverguje ... jestliže je rovna 0 ... tak buď konverguje nebo diverguje .. a musí se použít jiné kritérium .. tzn ... že suma 6 n=1 do nekonečna diverguje. a ta druhá .... ta vypadá : 1+2+3+4+5+6+7+8+9 ... no ... a lim j-->nek (j) .. no .. a ta limita je rovna nekonečnu .. tzn,že diverguje taky. :)

V třetím řádku překlep ... lim n--->nek .. ne lim x--->nek