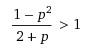Řešení nerovnice

Ahoj,nejdříve určíš podmínku.A řešíš nerovnici pro dva případy .... pro případ x>-2 a pro případ x<-2

Ahoj, díky moc, myslel jsem si to.. zkrátka se udělá co nejméně nulových bodů, v tomto případě jde udělat jeden ze jmenovatele a tím získám ty dva intervali. Pak dosazením zjistím, který je platný :)

Existuje i jiné řešení?

Napadlo mě se zbavit zlomku tím, že celou nerovnici vynásobím 2+p..

Musím si však uvědomit, že p může být kladné i záporné, takže řeším dva případy a to 2+p>0 a 2+p<0

Ahoj, lze se vyhnout tomu rozdělování na dava případy, když odečteme 1 a řešíme tabulkou metodou, kdy podíl dvou výrazů je kladný právě tehdy, když jsou oba dva záporné nebo kladné, jelikož -p^2-p-1 bude vždy záporné, zkoumáme, kdy je p+2 také záporné, tj. K=(-nek;2). Doufám, že se nepletu :-)

No .. jednoduše musíš zjistit ... nejlepší je tabulková metoda .. řekl bych... kdy jak čitatel tak jmenovatel bude kladný a nebo záporný.. a proto určíš nulové body.Zaneseš je do té tabulky a docela lehko to vyřešíš.Mrkni se na některé z Markovo videí na nerovnice. :)

Je to přesně tak jak říkám Martin. :)

Jinak ... tím rozdělením na dva případy ... měl bys pro

p>-2 : 1-p^2>2+p 0>p^2+p+1

no .. ale p^2+p+1 ... nikdy nemůže být záporné číslo...ani 0.. tzn,že tahle nerovnice nemá řešení.

a pro případ p<-2

máš 1-p^2<2+p 0<p^2+p+1 ... no ... a tahle nerovnice má zase nekonečně mnoho řešení .. ale víš,že je to jen v případě p<-2 ... tzn ... že můžeš za p dosadit jakékoliv číslo z intervalu (-nek,-2) a nerovnost bude platit.

P.S. Přepsal jsem se, má tam u mě být (-nek; -2 ), jak píše Vladan :-)

P.S. číslo 2 Přepsal jsem se taky... má tam být přesně jak říká Martin ... to je tak,když člověk si nečte po sobě co vlastně napsal.

Jj díky hoši :)

Ono v podstatě v tomhle konkrétním příkladě si stačí stanovit ty podmínky a jde to z toho vykoumat :)

Problém je, že když člověk něco potřebuje spočítat narychlo a zná nějaké zavedené postupy, tak počít počítá a ani si neuvědomí, že díky jednoduché úvaze to jde rychleji :)

Ono stejně řešit tohle tabulkovou metodou pro čitatele (který bych si rozložil) i pro jmenovatele není zrovna nejrychlejší rešení vzhledem k počtu intervalů :)

Ale jde to udělat tabulkově jen pro jmenovatele a tím se počet intervalů podstatně zkrátí :) každpodáně nejrychlejší úvaha je si celou rovnici vynásobit jmenovatelem a uvědomit si, že ten jmenovatel s neznámou může být kladný i záporný :)