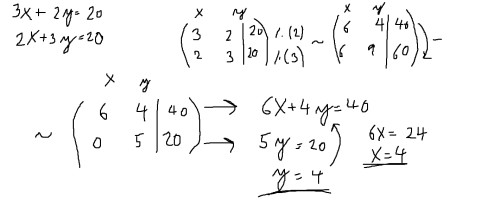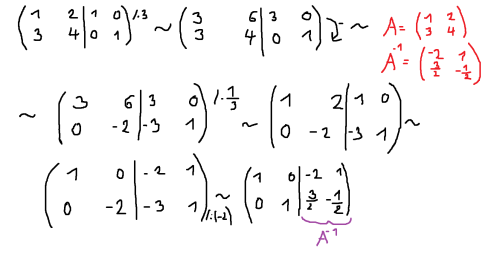Gaussova eliminační metoda

Ahoj Franto .... Gaussova eliminační metoda se používá pro výpočet determinantu matice... nebo výpočet inverzní matice... a výpočet soustavy rovnic ... máme matici ... a determinant se dá spočítat tak ... že když pod hlavní diagonálou budou nuly ... tak determinant je roven součinu prvků na té hlavní diagonálé .... Jak to máš na obrázku .. determinant by byl roven x1,1*x2,2,*x3,3 ... No ... a jak se k tomu dostaneš ? můžeš násobit kterýkoliv řádek ... jakýmkoliv číslem. .. ale jakmile řádek vynásobíš ... tak se ti znásobí i determinant tím číslem,kterým jsi násobil řádek ... vlastě jediný co děláš .. je násobíš ... sčítáš a odečítáš řádky matice ... tak ... aby jsi pod diagonálu dostal nuly... jak ve výpočtu inverzní matice,determinantu,tak i v soustavě linearních rovnic.

Přesně jak to mám tady .... počítám soustavu dvou rovnic o dvou neznámých... (ostatní by strašně dlouho trvali v malování) a já chci dostat nulu pod hlavní diagonálu ... jen jeden prvek je pod hlavní diagonálou .. a to je prvek v 2.řádku,1.sloupci ... takže násobím řádky tak ... abych je pak od sebe mohl odečíst .. a tím docílím toho,že mi tam vznikne ta 0.a řešení té soustavy už vidím... kdybych chtěl počítat determinant... musím si pamatovat čím vším jsem to násobil ... a pak to vydělit .. vidíš,že determinant téhle matice .. je 3.3-2.2 tj 5 ... a když se mrkneš na tu poslední matici co mi vyšla ... tak determinant je ... součin prvků na hlavní diagonále.. tj.. 6.5=30 .. ale první řádek jsem násobil 2 a druhý 3 .... tzn. že to musím vynásobit mezi sebou 2.3=6 .. a právě tou šestkou musím determinant té matice který nam vyšel vydělit .. a tím dostanu determinant původní matice.. tj 30/6=5

Ještě bych doplnil ... že při těch soustavách.... zápisuješ jednotlivé koecifienty do sloupců ... jak vidíš na obrázku nahoře ... mrkneš se jaký je koecifient u x na prvním řádku .. tj 3 .. u y je to 2 .... a na druhém řádku u x je 2 a u y 3 ... a nesmíš zapomenout na výsledky ... jinak by ses k ničemu nedopočítal .. a když násobíš řádek .. tak musíš násobit i "pravou stranu" té rovnice... tj ten výsledek... čemu se to 3x+2y rovná .. anebo 2x+3y čemu se rovná. :)

A k těm inverzním maticím .... když chceš určit nějákou inverzní matici .. k Matice A .. Tak si jednoduše napíšeš matici A ... vedle napíšeš jednotkovou matici .... a ty se z té matice co máš .... snažíš udělat matici jednotkovou,jednotková je taková,která má na hlavní diagonále jedničky ... všude jinde 0 ... jakmile něják upravíš tvojí matici A ... tak musíš tu samou úpravu provéct na té jednotkové matici vedle ... viz obrázek.

Děkuji moc, za vyčerpávající odpověď, teď to jen schroustat v hlavě a počítat a počítat. ;)

Díky!

Rádo se stalo :) jak sám říkáš .. stačí si spočítat pár příkládků .. a příjdeš tomu na kloub. :)

Františku, kdybys potřeboval video návod, tak Gaussova eliminační metoda je součástí mého kurzu Lineární algebra I.