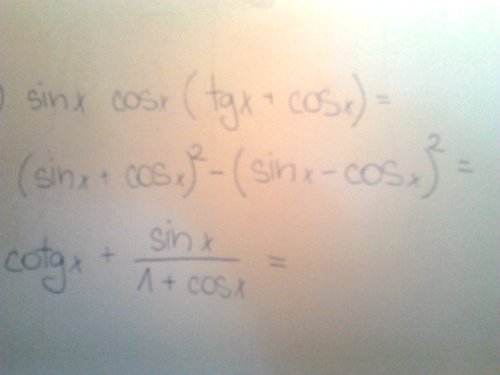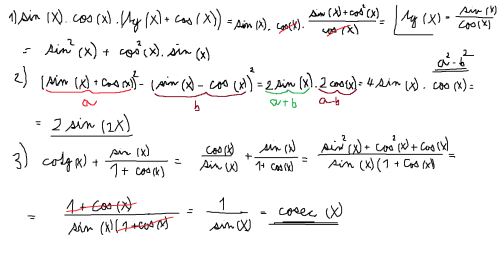Úprava goniometrických výrazů

Ahoj,1. příklad ... přepíšeš tg (x) jako sin(x)/cos(x) ... sečteš sin(x)/cos(x) s cos(x) (společný jmenovatel) .. pokrátíš cos(x) ... a zbyde ti tam sin^2(x)*cos^2(x)*sin(x) ... ten 2. použiješ a^2-b^2=(a+b)(a-b) ... dostaneš 4sin(x)*cos(x) ... no .. a máš vzorec : sin(2x)=2sin(x)*cos(x) .. vidíš .. že 4sin(x)*cos(x) je dvojnásobek .. tzn 4sin(x)*cos(x)=2sin(2x) .. a třetí ... přepíšeš cotg(x) jako cos(x)/sin(x) ... sečteš s druhým zlomkem (společný jmenovatel) dostaneš (sin^2(x)+cos^2(x)+cos(x))/((1+cos(x))*sin(x)) ... víš že sin^2(x)+cos^2(x)=1 .. tzn čitatel se zjednoduší na (1+cos(x))/((1+cos(x))*sin(x)) no .. teď vidíš.. že se ti 1+cos(x) pokrátí .. zbyde ti 1/sin(x) ... a 1/sin(x)=cosec(x) ..

Děkuji. nyní se to zdá až příliš jednoduché že? :)

Hezké znalosti