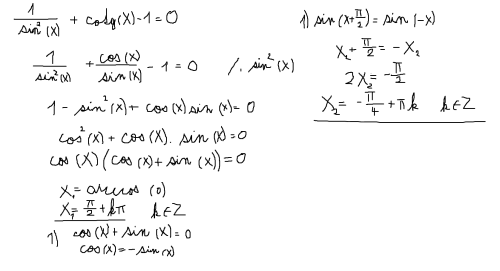Goniometrická rovnice

Cotg napiš jako cosinu / sinus. vynásob celou rovnice sinem na druhou. Jedničku napiš jako sinus na druhou + cosinus na druhou. Vytkni cosinus. dořeš jednoduchý rovničky. vím že je to popis na prd, ale mám teď asi 2 minuty. Kdyžtak napiš jestli to není srozumitelný. hodím se postup.

Aha, já se v tom hrozně zamotal, jsem to dával pod společý zlomek atd..

akorád na konci vytknout sinus a né cos :)

Zkusím jak to vyjde :) děkuju

Tak my vyšlo

1. sin x = 0 a 2) cos^2 (x) + cos x = 0 a to za druhé se zase rozdělilo na cos x=0 a cos x = -1

Problém je, že my vyšel výsledek (pík)/2 čili násobky 90stupňů, ale ve výsledcích je (pí/2)+kpí a (3/4)pí+kpí

Ahoj Jakube,je to přesně jak říká Marek.Nejprve přepíšeš cotg(x) jako cos(x)/sin(x),vynásobíš rovnici sin^2 (x),všimneš si,že se tam pak nachází 1-sin^2 (x)a to je přeci vzorec.1-sin^2(x)=cos^2(x),tak to tím cos^2(x) nahradíš,vytkneš cos(x) a máš to v součinu a vidíš,že to nula bude vycházet v dvou případech,když cos(x) bude 0 a když cos(x)+sin(x) bude 0,tak jednoduše pak dořešíš rovnice cos(x)=0 a sin(x)+cos(x)=0. Přikládám výpočet.

Díky moc :)

Já jsem dělal chybu při tom vytýkání, protože jsem přehlédnul, že tam je sin^2 - sin^2 a neodečetl jsem je :)

Rádo se stalo.Ještě by šlo použít vzoreček 1/sin^2(x)=1+cotg^2(x),když to nahradíš,tak dostaneš : 1+cotg^2(x)+cotg(x)-1=0 jedničky se ti vyruší a máš : cotg^2(x)+cotg(x)=0,no a nakonec vytkneš cotg(x),takže rovnice bude vypadat : cotg(x)(cotg(x)+1)=0 a teď si tu rovnici můžeš zase rozdělit a řešíš : cotg(x)=0 a cotg(x)=-1 a dojdeš ke stejnýmu výsledku. :)

Jj díky :) můžu se zeptat, kde jsi tenhle vzoreček sehnal? :)

Máš vzorec : 1=sin^2(x)+cos^2(x) ,tak to jednoduše vydělíš sin^2(x) a dostaneš : 1/sin^2(x)=sin^2(x)/sin^2(x)+cos^2(x)/sin^2(x) . Takže 1/sin^2(x) =1+cotg^2(x),protože cotg^2(x)=cos^2(x)/sin^2(x).