Křivkový integrál

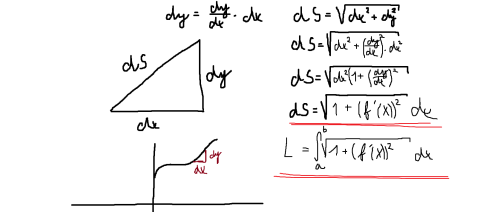
Ahoj Honzo,řekněme že vzdálenost mezi bodem xi a xi-1 bude nějáké "h",co se stane,když h pošleme k 0 ? Vzdálenost mezi bodem xi a xi-1 bude nekonečně malá,takže můžu říct,že ta vzdálenost je dx.To samé se děje i s f(xi) a f(xi-1),budou nekonečně blízko u sebe,takže můžu říct,že vzdálenost je dy.Teď se podívej na tu křivku S,pomohli jsme si něják tím dx a dy ? Pomohli,můžeš využít Pythagorovu větu k výpočtu dS,vidíš že se ti tam vytvoří pravoúhlý trojúhelník,který má odvěsny dx a dy a přeponu dS,to znamená,že dS^2=dx^2+dy^2 , po odmocnění máme : dS=odmocnina (dx^2+dy^2) a teď je víc možností,jedna z možností je to rožšířit výrazem dx/dx a druhá vědět,že dy=dy/dx * dx ,tím pak můžeš nahradit to dy a krásně ti tam výjde ta odmocnina (1+(dy/dx)^2) dx ,takže máme : dS=odmocnina (1+(dy/dx)^2) dx .My chceme ale vědět jak je křivka dlouhá na intervalu (a,b),takže to můžeme jednoduše zintegrovat a určit tomu meze,Jaký budou meze? No,právě ty krajní body toho intervalu,přesně tak jak je to na obrázku.Doufám,že je to srozumitelné,Vladan.

Myslím,že je tohle mnohem jednodušší postup,jak s tou větou o střední hodnotě.Jinak,jak jsem vytkl to dx^2,tak mi na konci chybí závorka,omlouvám se. :)

Ok, chapu. Diky moc :).