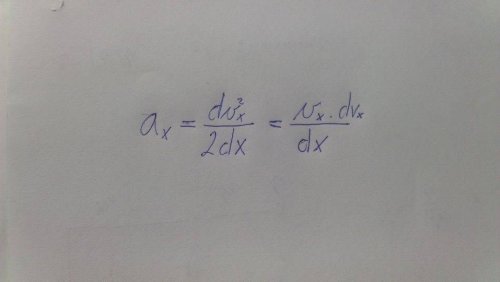Derivace rychlosti
Zdravím, potřeboval bych vysvětlit vztah na přiloženém obrázku. Jedná se o výpočet zrychlení ve vodorovném směru x z derivace rychlosti ve vodorovném směru.Jde o příklad který jsme dnes počítali ve škole. Vím že rychlost se vypočítá jako derivace dráhy podle času a zrychlení jako derivace rychlosti podle času. Jenže v tomto případě jsme počítali derivaci kvadrátu rychlosti podle dráhy. A nechápu právě proč je to podle dráhy, proč je v tom vztahu to dx a ještě u toho ta dvojka ? Ten vztah je dále rozepsán, ale ani v tom rozepsaném tvaru ho nechápu. Díky za rady :)
Jan K.
14. 04. 2015 18:35
6 odpovědí
Ahoj, ta dvojka znaci druhou derivaci protoze druhou derivaci zrychleni dostanes drahu, musis si to dat prave do souvislosti: derivace rychlosti je draha, derivace zrychleni je rychlost a kdyz zderivujes tu rychlost tak dostanes drahu, takze kdyz udelas druhou derivaci zrychleni dostanes drahu
Jinak bacha jak reknes ze to je kvadrat tak to neni pravda znaci tu druhou derivaci s kvadratem to nema nic spolecneho, to by muselo byt u x ta dvojka, nekdy se to taky znaci bud carkamu kolikata je to derivace, nebo tady taky je moznost teckama co znaci derivaci v case.
Jirko, prosimtě já už jsem teda fyziku neměl ani nepamatuju, ale jaktože druhá derivace zrychlení je dráha? Není to náhodou naopak? A hlavně tady je to celý nějaký divný, protože se derivuje podle dráhy a navíc ta symbolika je nějaká divná.
Já vím jak dostat pomocí derivací z dráhy rychlost a následně zrychlení, ale tento vzorec nám učitel napsal na tabuly při řešení jednoho příkladu. K té symbolice, ten dolní index "x" u rychlosti mi značí že počítám s x-ovou složkou vektoru rychlosti. A druhá derivace to být nemůže, protože to by ta dvojka v exponentu musela být u písmena d. Bylo mi na hodině pouze vysvětleno že je to opravdu kvadrát rychlosti derivovaný podle dráhy. Nechápu ale jak ten vztah vznikl. Z nebe přeci nespadl. Chápu derivaci rychlosti podle času, ale podle dráhy ? To mi nic neříká.
Hele asi jsem na to přišel, ale nejsem si tím úplně stoprocentně jistej. Úvaha ja následující:
místo x používám s
F=ma
Ek=1/2mv^2
Ek=F.s (působim silou F po dráhu S, tím vykonám práci W, která je rovna kinetické energii, protože tam nejsou žádné ztráty.
mas=1/2mv^2
as=1/2v^2
zderivuju podle s
a=1/2*dv^2/ds
to za tím druhým rovníkem už je jenom provedení té derivace.
Díky, to by snad mělo být ono, jinak už netuším :)