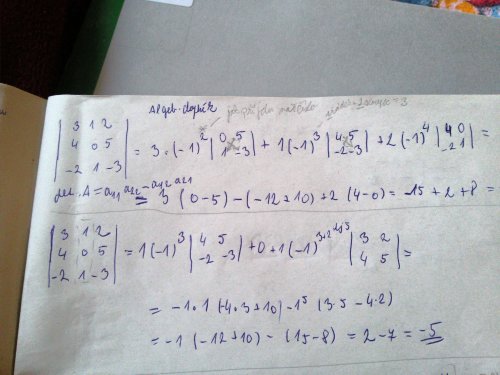Matice
Dobrý den, chci se zeptat proč se řešil první příklad tímto způsobem. A u druhého příkladu se chci zeptat když roznásobuju derminat 4 * (-3) a 5 * (-2) ..proč ve výsledku je v závorce (-12+10)
Klára B.
21. 04. 2015 08:35
6 odpovědí
Ahoj Kláro,proč bychom nemohli použít jiný způsob ? Právě tím je matematika krásná,dokážeš se dopočítat k výsledku mnoha způsoby.Sice tak,jak to počítáš v druhém příkladě mi to příjde rychlejší a méně pracný.
Spíš nechápu proč.. když násobí čísla 4 * (-3) a 5 * (-2) ..tak by mělo vyjít (-12 a -10) a ne -12+10
Protože determinant matice 2x2 spočítáš tak,že vynásobíš prvky na hlavní diagonále a odečteš od toho součin prvků na vedlejší,takže když bereš tu první matici,tak násobíš : 4*(-3)=-12 a součin prvků na vedlejší diaogonálé je : 5*(-2)=-10,ale ty ten součin musíš odečíst,takže máš -12-(-10)=-2,pak před tím máš ještě tu (-1),takže se ti znovu obrátí znaménko a tím pádem dostaneš 2 a když od toho odečteš tu 7,tak dostáváš determinant té matice 3x3 a ten je právě těch -5.
Aha jasně..takže se to vlastně pokaždé odečítá. Je to tak? :) ..myslím v těch závorkách
Ano,vždy vynásobíš prvky na hlavní diagonále a odečteš součin prvků na vedlejší diagonále,ale to platí jen u matice 2x2,u matice 3x3 se využívá buď Sarrusovo pravidlo,Gaussova eliminační metoda anebo právě Laplaceův rozvoj podle řádku/sloupce.U matic 4x4 a výš se to už dá spočítat jen skrz Laplaceův rozvoj (hrozná dřina) anebo eliminační metodu.
Děkuju :)