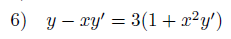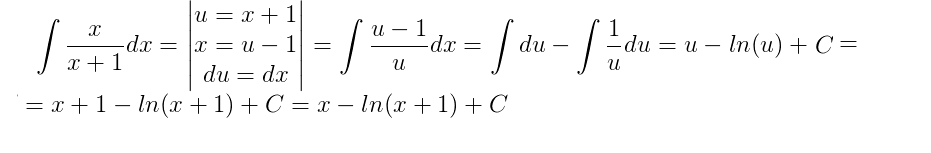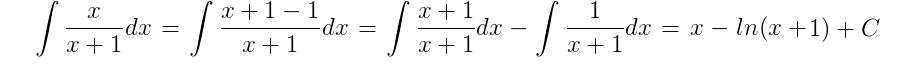Variace konstanty

Ahoj Michale,

jestliže to chceš počítat přes metodu variace konstanty,tak danou rovnici musíš dostat do tvaru y'+p(x)y=q(x).Takže v našem případě stačí roznásobit závorku na pravé straně,přičíst k rovnice xy' a následně pak odečíst y a 3,pak stačí vytknout y' a celou rovnici vydělit výrazem u y',a tak to převedeme do tvaru y'+p(x)y=q(x).Nyní vynulujeme pravou stranu a budeme řešit rovnici y'+p(x)y=0,takže stačí odečíst p(x)y a rovnici vynásobit výrazem dx/y,pak to celé zintegrovat.Získáme obecné řešení naší rovnice.Obecné řešení bude ve tvaru : yo(x)=C.a(x).Teď nám už jen zbývá řešení partikulární,protože my jsme přeci řešili rovnici nezávisle na té pravé straně,takže by nám to nemohlo vyjít.Partikulární řešení bude ve tvaru : yp=C(x).a(x). C bude nějáká funkce proměnné x,kterou my potřebujeme zjistit.Budeme yp dosazovat do rovnice y'+p(x)y=q(x).Z toho se dá vidět,že potřebujeme zjistit i yp',což není zas tak složitý úkol,stačí použít derivaci součinu : yp'=C'(x).a(x)+C(x).a'(x).Teď tam stačí dosadit vše co známe,vyřešit rovnici a tím zjistit C(x) a jsme hotovy.Našli jsme řešení partikulární,a tím známe celkové řešení rovnice,které bude ve tvaru : y(x)=yp+yo (partikulární+obecný).Doufám,že jsem pomohl,kdybys něčemu nerozuměl nebo ti příklad nešel vypočítat,tak napiš,Vladan.

Jinak,co se týče toho per partes,určitě by to šlo,ale příjde mi to zbytečně složitý oproti substituci,ten příklad máš vypočítaný v příloze,pokud bys to chtěl počítat per partesem,tak bych si vzal : u=x , du=dx , dv=1/(x+1) , v=ln(x+1).Musel bys využít per partes dvakrát,pak ještě u integrálu ln(x+1)dx.

Ahoj s tou variací díky moc, už chápu jak na to, jen se chci zeptat k tomu druhýmu příkladu nerozumím te substituci x=u-1 proč zrovnu u-1?

Vycházel jsem z u=x+1,když odečteš jedničku od obou stran,tak dostaneš x=u-1.Ještě by ten integrál šel udělat takto,ale je to víceméně to samé,jen nepoužíváš substituci.