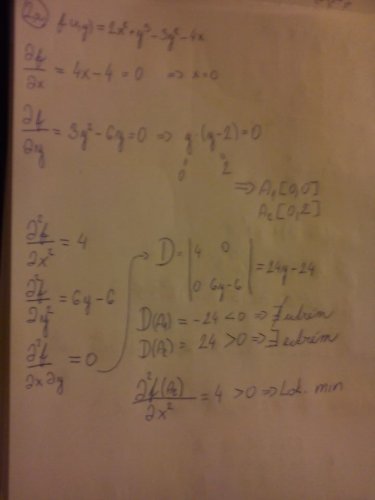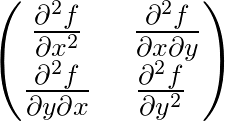Lokalne extremy - stacionarne body

Ahoj Evo,

je to hodně obdobné jako u funkce jedné proměnné.Stačí funkci parciálně zderivovat podle x ,podle y a dát parcialní derivace rovny 0,vyřešit soustavu rovnic,která vznikne,a tím zjistít stacionární body.Teď nás bude zajímat,jestli jsou v bodech,které nám výjdou,extrémy nebo sedlové body.Sestrojíme si Hessovo matici(v příloze máš její tvar,když počítáme extrémy nebo sedlové body funkcí dvou proměnných)(samozřejmě dosazuješ do parc. derivací bod,který zkoumáš) a spočítáme Hessián (determinant matice).Pokud bude Hessián větší jak nula,jedná se o extrém.Pokud bude Hessián menší jak nula,jedná se o sedlový bod.Teď nám už jen zbývá určit (pokud nám výjde,že Hessián je větší jak 0),zda-li je v bodě lokální minimum či maximum.Stačí vzít druhou derivaci funkce podle x a dosadit bod,který zkoumáme,jestliže je hodnota této derivaci větší jak 0,tak se v tomto bodě nachází lok. minimum,pokud nám výjde záporná hodnota,jedná se o lok. maximum.Doufám,že jsem pomohl,Vladan.