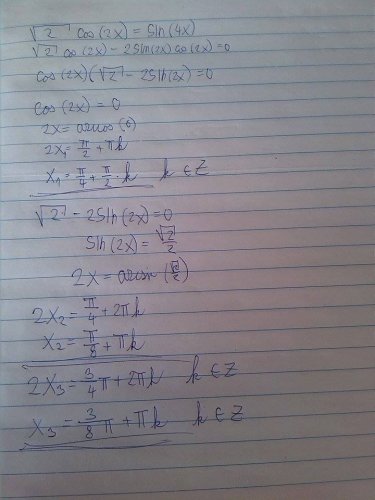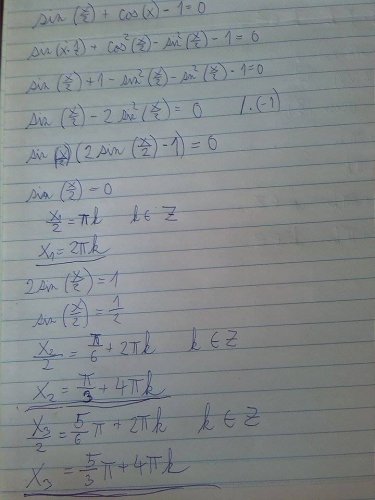Goniometrická rovnice

Ahoj,

sin(4x) jsem přepsal jako 2sin(2x)cos(2x),odečetl jsem ho a vytknul cos(2x) a vyřešil dvě jednoduché rovnice.Doufám,že to pomohlo,výpočet přikládám do přílohy.

Děkuji za výpočet, jen mi není jasné, proč je u x1 řešení (pí.k)/2

Když je cos, tak je perioda 2pí. Proč je to tady jinak? Děkuji za odpověď. :-)

A ještě jestli bych mohla poprosit o výpočet tohoto příkladu: sin x/2 + cos x -1 = 0

Dobrý den Moniko, nejsem zdatný gonimetr, ale ten poslední příklad, co píšete, mi vyšel cos x = 1 nebo cos x = 1/2. Řešil jsem to tak, že jsem si sin x/2 napsal jako: odm((1-cos x)/2). A pak jsem to už jen upravil, zavedl substituci cos x = a; a řešil jsem kvadratickou rovnici, jejíž kořeny jsem již výše napsal. Ty periody ať jsem radši napíše Vladan, já v tom moc pevný nejsem :-) Co se týče té periody, můj skromný odhad je, že ne vždy je ta perioda 2pí, záleží na tom kde se na tom grafu pohybujeme. http://cs.wikipedia.org/wiki/Kosinus#/media/File:Cos… Doufám, že jsem alespon trochu pomohl :-)

Ahoj,

u řešení x1 je (pí.k)/2,protože cos(x) nabývá hodnoty 0 po periodě pí,když se koukneš na graf,tak to vidíš,ale je to vyjímka,jinak má periodu 2pí(pokud je v argumentu holé x).V příloze je výpočet druhého příkladu,použil jsem vzorec dvojnásobného úhlu,abych přepsal cos(x) a poté jsem použil goniometrickou jedničku(je dobré trocha koukat dopředu,věděl jsem hned na začátku,že se mi jedničky odečtou),upravil,vytknul a vyřešil jednoduché rovničky.Perioda se mění v závislosti na argumentu té funkce.Jestliže máš sin(x/2),tak perioda nebude 2pí,ale 4pí,protože se růst (i pokles) zpomalí na polovinu a kdybys měla dejme tomu sin(2x),tak perioda bude pí,protože funkce bude růst (i klesat) dvojnásobně rychleji,Vladan.