Variace s omezením
Dobrý den, zajímalo by mě, jak je nejlepší řešit příklady následujícího typu:
Chci vytvořit slovo dlouhé 10 znaků, jediné povolené znaky jsou A, B a C. Nesmí se stát, aby A sousedilo s B i C najednou. Kolik slov můžu vytvořit?
Potřeboval bych nějaký elegantní způsob, který bych mohl aplikovat i na složitější příklady s více omezeními. Díky!
Matěj K.
24. 07. 2015 11:48
8 odpovědí
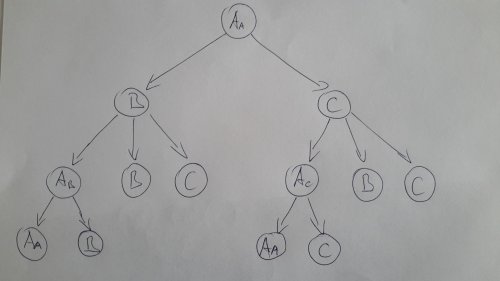
Ne, ze by to bylo uplne reseni, ale napada me napriklad pouziti takovehoto vyvojoveho diagramu. Aa znaci ze muze nasledovat B i C, Ab znaci zeje to Acko, ktere nasleduje po Bcku, takze nesmi nasledovat Ccko. Takze mame zachycene vsechny mozne cesty a kdyz narazim na nejake pismenoa diagram konci, skocim na stejne pismeno v diagramu vyse a opakuju postup. Ale jak z tohodle spocitat pocet moznych retezcu to fakt netusim. To by chtelo nekoho kdo se dobre vyzna v diskretni mstematice a to ja teda rozhodne nejsem :-).
K tomuto jsem ještě došel :) Ale díky!
Ahoj, pokud ti bude stačit jen přibližné řešení bez elegantního řešení, tak můžeš napsat program, které všechny varianty prostě prozkouší a spočítá. Pokud bude dobře navržen, tak není problém vygenerovat třeba 300 tisíc variant každou sekundu.
Tak můj program to zvládá za 16 ms, ale takhle to řešit je hodně trapný :D Každopádně Tvůj příspěvek mě donutil se nad tím znovu zamyslet a myslím, že jsem na stopě řešení.
Matěji, tak se pak o to řešení prosím poděl. Sám jsem na to hodně zvědavej. :-)
No, sice nejsem matematik, pouze laik, ale co říkáte na tuhle teorii? Od základu všech kombinací bez podmínky, tedy 3^10, odečíst počet nemožných kombinací. Využil bych při tom faktu, že pokud dojde na nějaké pozici ke změně znaku oproti předchozímu, počet možných následujících znaků se sníží z původních 3 na 2 možné. Dále je tedy potřeba spočítat počet kombinací pozic, kde může nastat změna oproti předchozímu znaku, což bude 9! (na první pozici změna být nemůže). Výsledek by pak tedy byl (3^10)-9! = 362880. Za správnost absolutně neručím, jen mě tato úvaha napadla. Těším se na Vaše názory.
Matěji, naprosto všechny příklady, které počítáš ve škole, mají tu výhodu, že byly zvoleny pro svoji jednoduchost.
Díky tomu dokážeš všechna zadání spočítat v řádu minut a nemusíš se trápit.
Pokud si ovšem příklad vymyslíš sám, už to neplatí.
Tvoje zadání vůbec není jednoduché spočítat a trvalo mi dva týdny na to přijít.
Nakonec mě napadlo použít vektorové stavové automaty pomocí skrytých Markovových modelů.
To je mechanismus, který má paměť předchozích znaků a predikuje následující znaky na základě historie.
K tomu stačí sestavit matici o velikosti 27x27 a umocnit ji na 12-tou, abys dostal všechny možnosti o délce 10.
Bohužel, je to hodně komplikované na výpočet i na vysvětlení, ale stále je to v lidských silách.
V podstatě se pohybuješ v nějakém pravděpodobnostním prostoru dokud nezafixuješ finální stav.
Tím zjistíš, s jakou pravděpodobností ses tam mohl dostat a z toho ihned plyne počet možných řešení.
Každopádně díky za zajímavé zadání.
Ještě se mi povedlo zjednodušit model, nakonec stačí matice 9x9, která vypadá takhle:
[[1 0 0 1 0 0 1 0 0] [1 0 0 1 0 0 0 0 0] [1 0 0 0 0 0 1 0 0] [0 1 0 0 1 0 0 1 0] [0 1 0 0 1 0 0 1 0] [0 1 0 0 1 0 0 1 0] [0 0 1 0 0 1 0 0 1] [0 0 1 0 0 1 0 0 1] [0 0 1 0 0 1 0 0 1]]
Jejím umocněním na N-tou je na pozici (0, 0) počet možných řetězců o délce (N-2).