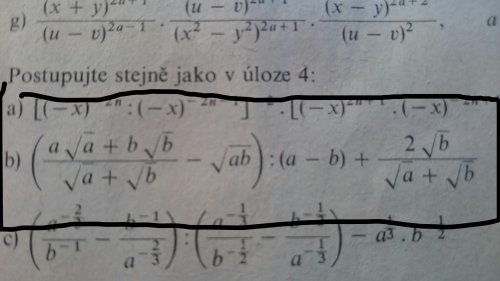Úprava výrazu

Ahoj Josefe,

pokdu si měl na mysli příklad b), tak já bych sečetl věci v první závorce, vydělil bych ji (a-b), a pak bych to celé sečetl s tím výrazem na pravé straně se společným jmenovatelem (sqrt(a)+sqrt(b))×(a-b). Je důležité si uvědomit, že a krát b, to celé pod odmocninou je to samé jako, odmocnina z a krát odmocnina z b, pak tam nějaké ty odmocniny zmizí. Po těch dvou sečtení tam nahoře vznikne něco, co je třeba posčítat. Nakonec je třeba se snažit to nahoře rozložit na součin, aby se to dalo krátit s tím spodkem. Myslím, že by si to po tomhle už mohl vypočítat. Mně osobně to vyšlo 1 pro a,b > 0, a nerovno b (nebo jinými slovy všechny body roviny z prvního kvadrantu se souřadnicemi [a,b], mimo poloos a přímky b=a, tj. osa prvního kvadrantu) Pokud by to stále nešlo, dej sem svůj výpočet, aby bylo vidět, kde děláš chybu. P.S. Ty blbosti s těmi kvadranty nemusíš vnímat, pokud jste nic takového nedělali, sám si tím nejsem tak jist. Je to vlastně graficky definiční obor toho výrazu, nebo si to alespon myslím :-)

Martin

Ještě ten výpočet, poprvé se mi to nepřipojilo.

Ahoj Josefe,

mě to vyšlo také 1, ale podmínky jsou podle mě a, b>= 0, a<>b, protože základ odmocniny můžete byt i nula. Schválně zkus dosadit a=9, b=0 a výraz má smysl, nikde nedělíš nulou, ani nemáš záporný odmocněnec. K tomu krácení, jak píše Martin, jsem se nějak nedobral, možná by se našel efektivnější postup.

Máš pravdu Karle :-) Omlouvám se za případný zmatek. Psal jse to ve spěchu, myslel jsem si to dobře a nakonec to napíšu špatně (ještě si řikám že a i b může být nula, jedný případ, kdy nám to "vadí" je, když jsou obě proměnné nula, ale to jsme vyřešili tím, že a je nerovno b) :-) Díky za opravu Karle, mimochodem to krácení je na konci, ty jsi to roznásobil ve jmenovateli, já to rozložil na součin v čitateli :-) Krátili jsme na konec oba. Ale na druhou stranu myslím, že pokud by se tam zkrátilo jenom třeba to (a-b), po tom roznásobení by to tak vidět nebylo. Problém je v tom, že nemůžu říct, že v součinu je to vždy lepší, někdy se to prostě vyplatí roznásobit. V tom je právě ta matika pro lidí většiou protivná: není jeden daný postup, je třeba přemýšlet. Ale každý jsme nějací, mně to třeba přijde krásné :-) Jinak kdybych ti měl něco poradit Josefe, nikdy u úpravy výrazů nespěchej, ikdyž se ti zdají sebelehčí. Vždy dělej s rozmyslem každý krok. Což je mimochodem uneverziální rada pro jakoukoli matematickou (i fyzikální) úlohu. Ne vždy je totiž chyba v tom, že si nedodržel matematická pravidla. :-)Přeji hodně zdaru v matice! :-)

Martin

Děkuji,už vím co jsem dělal špatně,jako jmenovatele jsem v celkovém dělení bral celý pravý výraz,nedošlo mně,že není v závorce,tudíž musím nejdřive dělit a potom přičítat.Taková zásadní věc a mně to nedošlo!!