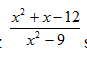Výraz

Ahoj, řekl bych, že řešení je prosté.

Toto řešení já mám, ale ve výsledcích je X+4/X-3. Proto jsem se radči ptal.

I mistr tesař se někdy utne. Máš to správně. Pokud si to chceš opravdu ještě jednou ověřit, tak si to můžeš vydělit.

Ještě mně napadá takové méně matematické (ale přesto pro tento případ funkční) řešení, a to je v tom, že si prostě dosadíš pár čísel a uvidíš, že to vyjde stejně.

Máš pravdu. Díky

Honzo, dosazení čísla, abys zjistil rovnost, je velice matematické řešení :-)

S trochou formalismu a predikátové logiky:

tvoje úprava tvrdí, že pro každé x libovolné, pevné [v rámci def. oboru] platí rovnost L=R

to je ekvivalentní tvrzení, že neexistuje x libovolné, pevné [na def. oboru], aby platila nerovnost L≠R

ekvivalence tvrzení vytváří tautologii a pokud najdeme nějaké x, pro které platí nerovnost, nemůže platit původní rovnost

Takže, prosím, nezatracuj dosazení čísla jako nematematickou metodu, při správném použití je to efektivní zbraň a používá se velice často.

Myslel jsem to tak, že by v některých případech dosazení mohlo skutečně vyjít stejně a přitom jde o různé výrazy (pokud budeš špatně volit vhodná čísla).

Mějme například předpis: |x|=x

Tento předpis platí pro všechna nezáporná čísla. Pokud bychom čísla volili bezmyšlenkovitě (například jen přirozená čísla), tak dojdeme k špatnému řešení.

Chtěl jsem jen říct, že obecně dosazování není dobré, protože nelze žádným algoritmem jednoznačně určit, které množství hodnot je optimální a jestli náhodou není náhoda, že to vyšlo stejně (což se u obecného složitého výrazu hodně špatně určuje). Narazil jsem na to, když jsem navrhoval nový Mathematicator a hledal metodu, jak ověřit, že jde o totožné výrazy (musí se to dělat analyticky, "hrubá síla" tady funguje jen omezeně).

Myslel jsi to špatně a řekl jsi to také špatně [uf, to jsou silná slova].

Problém v tvém algoritmu spočívá v tom, že se neexistencí sporu pro existenční kvantifikátor snažíš dokázat platnost obecného kvantifikátoru - a co hůř, doména tvých funkcí je z principu nespojitá a omezená na podmnožinu racionálních čísel, což je obecný problém vznikající při každé kvantizaci do diskrétního oboru.

Na oba tyhle problémy jsem tě sám upozornil a ukázal ti protipříklady, vzpomínáš?

Jenže v případě domácího úkolu nemáme problém ani s jedním, jsme na reálných číslech a obě hyperboly se mohou protínat maximálně ve dvou bodech, což nás ale stejně nezajímá, protože dokazujeme spor v existenčním kvantifikátoru pro zcela zjevně různé výrazy. Více než dva pokusy nepotřebuješ.

Proč jsi to myslel špatně? Protože zobecňuješ nesouvisející případy.

Proč jsi to řekl špatně? Protože korektní [jak jen to slovo zdůraznit?] dosazení hodnot pro existenční kvantifikátor je velice matematické.

Hádám, že teď jsi někde v prváku na vysoké, ne? Za pár měsíců bys tohle měl umět a budeš schopen rozlišit ty rozdíly.