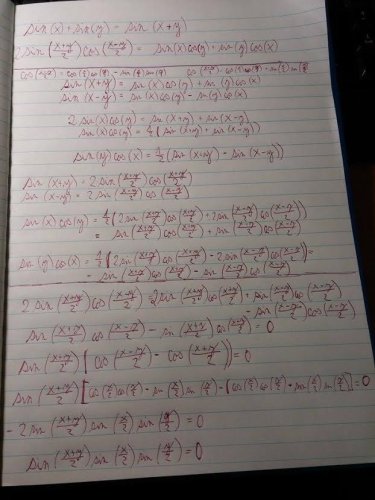Goniometrická rovnice

Ahoj Pavle,

je to dost těžký. Zatím nevím jak na to :-). Napíšu Vladanovi. Třeba si s tím poradí.

Marek

Marku děkuju :)

Napadlo mě to řešit jako dvě rovnice o dvou neznámých a druhou rovnici: cos(x) +cos(y) = cos(x+y),problem ale je že když to umocnim a pak sečtu,tak na leve straně mi vyjdou jedničky ale s pravou stranou si nedokážu poradit..

Omyl :)

Došlo mi,že je to dvojčlen takže to tak jednoduchý jak jsem psal to nebude :))

Pavle mám to.

platí vzorec sin(x+y)=sin(x)*cos(y)+cos(x)*sin(y)

a jelikož řešíš rovnici sin(x+y) = sin(x) + sin(y), tak musí platit, že cos(y)=1 a cos(x)=1

takže máš řešení x=2kpi y=2kpi.

Je to srozumitelné?

Marku děkuju :)

Jen se chci zeptat,není to jen jedno z řešení? Jestli počítáš s tím,že k je z množiny celých čísel,tak se ti ztratí kořeny,kdy je x(nebo y) rovno π (tudíž 0) a pak by daná rovnice taky platila.. sin(π+3π) = sin (π)+ sin(3π)

Ahoj Marku a Pavle,

před tím, než bych začal určovat řešení, tak bych si to využitím pár vzorců upravil. Má upráva je v příloze, z té formy, která vznikla, to jde mnohem lépe určit. Zbytek nechám na tobě, jestli by nebylo něco jasné, tak napiš.

Vladane díky. Ještě jsem nestačil postnout tvůj postup. Koukám, že ty dvě řešení máme stejně,a le že ti tam vychází ještě jedna sada řešení navíc. A dává to smysl.

Vladane a Marku moc děkuju,ve složitějších gon.rcích se ještě nechytám...to přijde :)

Mám ještě dvě otázky

1. Dalo se to řešit přes soustavu sin(x+y) =sin(x) + sin(y)

cos(x+y) =cos(x) + cos(y) ?

Zkoušel jsem to ale bohužel mi to nevycházelo,nevěděl jsem jak dál :/ 2) mohl bys mi objasnit postupy v tom prostředním (odděleno čarami) oddělení? Moc je totiž nechápu :/ + si nejsem jistej s řešením v posledním řádku,ale myslím že to ještě přijde :)

Napsal jsem si to a hned je mi to jasny :) Děkuju moc oboum! :)

Pavle, ještě k té druhé rovnici: cos(x+y) =cos(x) + cos(y)... ta přece není součástí zadání ne? Tak jí nemůžeš použít. To by sis jí tam vlastně přičaroval :-)...

Pravda :)

Jak tedy Vladan přišel na tu rovnici sin(x-y) = sin(x) - sin(y) to mi vrtá hlavou)

Dal si jí tam aby měl "hezkou" soustavu?

EDIT: Jasně může jí tam použít, protože je to vzorec :) v pohodě :)

Pavle, jsou to víceméně kombinace vzorců, snažil jsem se výraz převéct něják na součin a přišlo mi, že tohle bude nejjednodušší způsob, jak to provéct. Řešení se pak totiž určí jednoduše, stačí, aby jeden z tich výrazů byl roven 0 .