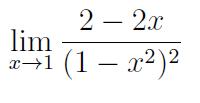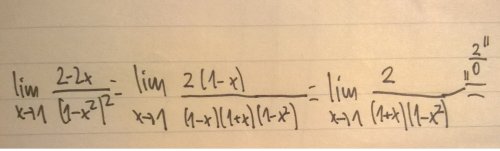Limita zprava a zleva

Ahoj Michale,

zkus to trochu pokrátit a hnedka uvidíš, proč se počítá levostranná a pravostranná limita.

No když jsem to počítal, tak jsem dostal 2/0 a to jsem bral že už je konec a výsledek je nekončeno. Takže i když po prvním dosazením (ze zadání dostanu 0/0) a pak někde něco/0, tak už musím počítat zleva a zprava? A pokud ano, tak počítám to od toho kroku nebo jakob od začátku? Díky

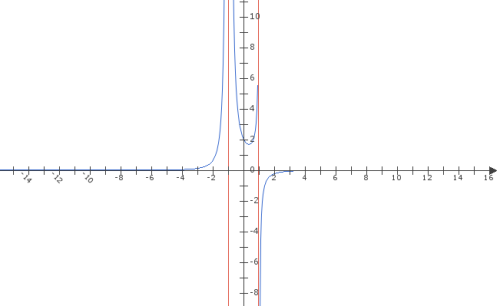
Koukni se na graf té funkce, z toho se dá jednoduše poznat, proč hledáme jednostranné limity. Hodnota jednostranných limit není stejná (liší se o znaménko), to znamená, že dvoustranná limita neexistuje.

Ještě doplním, že graf této funkce vypadá takto (limity jsou nádherně vidět):

K generování grafu jsem použil nový engine Mathematicatoru, který bude (snad) do pár měsíců veřejně přístupný.

A když z předpisu nevím jak graf vypadá, tak to asi nemám šanci že?

Jinak jak jsem psal včera, po 1. dosazením je to 0/0, tudíž alg. úpravy, poté to je 2/0 a to už znamená že oboustranná neexistuje, tudíž počítám zleva a zprava, že? A počítám to pro tu původní fci (ze zadání) nebo pro to co mi vyšlo po alg. úpravě?

Graf se dá přibližně odhadnout u podobných zadání skoro vždycky. Pokud to je zlomek, tak jako první vždy zkoumám definiční obor.

V podstatě to stačí roznásobit podle vzorečku (a+b)^2, vyřešit rovnici a rovnou vidím, kde by mohl být teoretický problém.

Takže vidím, že D(f) je R - { 1, -1} , a limita se blíží k 1, tudíž v jedničce to není definované a musím počítat zleva a zprava že?

Přesně tak. Pokud takové číslo nelze dosadit, tak tam limita existovat nemusí (to se musí ověřit, ale jako podezřelý bod to určitě stačí).

Abychom byli matematicky přesně správní, tak bychom dále měli ověřit spojitost (tj. jak moc se liší hodnoty funkce v bezprostředním okolí nedefinovaného bodu), ale to po tobě už asi ve škole chtít nebudou.

Pokud má nějaká funkce limitu v nějakém bodě n znamená to, že se limity v bodě n zleva i zprava rovnají. Pokud ne, musíme řešit zvlášť limitu zprava a zvlášť limitu zprava.

Ahoj, postup by měl být takto: pokusíš se do výrazu dosadit, když ti nevyjde neurčitý výraz, tak máš vyhráno, jinak se pokusíš výraz upravit, aby ses zbavil toho, co ti ten neurčitý výraz dělá. Pokud se ti to nepovede, tak rozděluješ na limitu zprava a zleva. Pokud se tyto limity rovnají, tak i limita v tom bodě je rovna limitě zprava resp. zleva, jinak limita v daném bodě neexistuje. :)