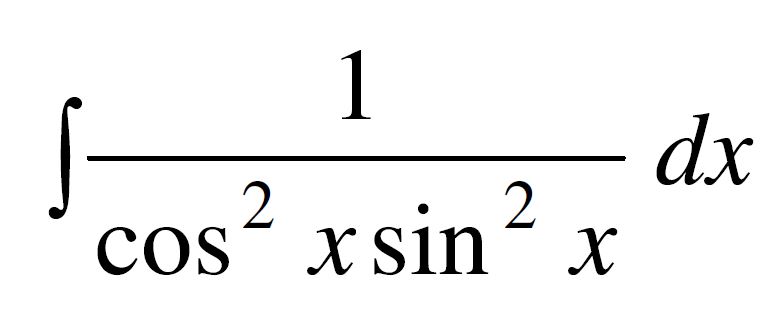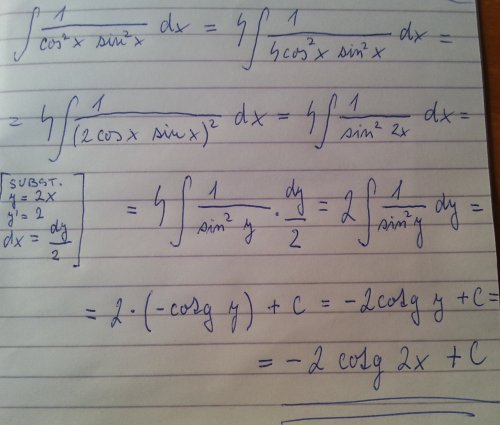Neurčitý integrál (sin cos)

Omyl. Vyjadroval som sa k inému príkladu :D pardon

2 * sinx * cosx = sin 2x

Pak už je to jen základní vzoreček.

Nevim to :/ postne tu niekto postup? Tápam :/

1 / (cos^2(x) * sin^2(x)) = 1 / (cos(x) * sin(x)) ^ 2 = 4 / sin^2(2x) = 4 * cosec^2(2x)

Tohle už je jen vzoreček z učebnice.

Ideš namňa moc odborne ... nerozumiem tomu... skús to napísať na papier... cosec^2 je co ?

Ahoj Radoslave, máš vzorec (1) sin(2x)= 2sin(x)*cos(x) , umocníš to celé na druhou a získáváš : (2) sin^2(2x)=4sin^2(x)cos^2(x) , všimneš si, že v integrandu máš ve jmenovateli zlomku sin^2(x)cos^2(x). proto z vztahu 2 vyjádříš cos^2(x)sin^2(x), krásně vidíš, že je to sin^2(2x)/4 . Teď to jednoduše nahradíš a budeš mít 1/(sin^2(2x)/4) = 4/sin^2(2x) a teď stačí vědět, že cosec(x)=1/sin(x) , proto cosec^2(2x)=1/sin^2(2x), takže výraz můžeš napsat jako 4cosec^2(2x) a teď to stačí zintegrovat, mohl bys vědět, že integrál 4cosec^2(x) je -4cotg(x)+C , ty tam máš ale cosec^2(2x), to znamená, že to musíš ještě vydělit dvěma, takže výsledek bude : -2cotg(2x)+C.

Ahoj, tady to máš vypočítaný :-)

Ahoj, vidím podobný příklad na goniometrické rovnice, mohl bych požádat o pomoc v řešní příkladu: Integrál 1/5+4cosx . Moc děkuju

Ahoj Davide, tvůj příklad je krapet jiný než Radoslava. Dobré by bylo použít substituci t=tg(x/2). Už se tu obdobný příklad vyskytoval. http://mathematicator.com/index.php?page=forum&a=143

Díky, zkusím se s tím poprat:-)

Kdyby byl problém, založ nové téma, rád ti pomůžu. :-)