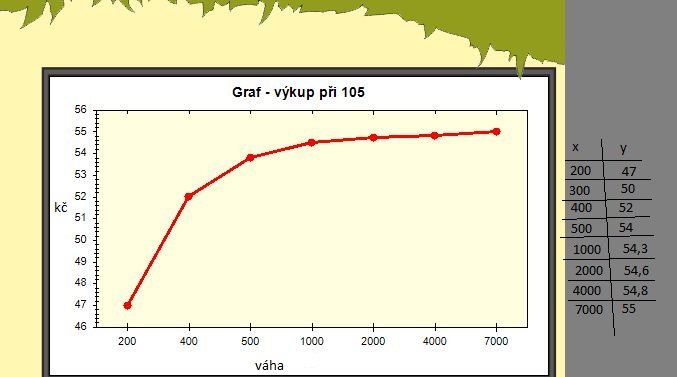
Zjištění funkce

Bez další znalosti o původní funkci je možné získat pouze hypotézu, to je funkce, která se co nejvíce bude původní funkci blížit.

A šlo by zde uvést tu hypotézu ? Nic víc k tomu nemám. děkuji

To není "ta" hypotéza, takových funkcí je hodně.

Spočítat to jde, ale pokud máš takhle málo dat, tak je nutné vědět, odkud data pochází, co má funkce vyjadřovat i jak se má používat.

A nakonec je to hodně práce, protože se taková funkce dlouho hledá.

Nicméně tento problém zajímá i mě, co když mám udělanou křivku, která už je grafem nějaké funkce, ale nevím jaké? Jak předpis takové funkce najdu?

Mikoláši, najdeš ji zkušenostmi, intuicí, štěstím a metodou pokus omyl.

Třeba velice častý postup je polynomiální regrese.

Řekneš si, že by data mohla být výsledkem nějakého polynomu.

Pak zkusíš uhádnout jeho stupeň.

Nakonec vytvoříš soustavu rovnic, která obvykle nemá řešení, a najdeš co nejlepší koeficienty polynomů.

Pokud mluvíš o křivce v souvislosti s funkcí, tak bys měl vědět, že tohle jsou hodně jednoduché funkce a funkcí, které by šly nakreslit, je jen velice málo. Funkcí, které nakreslíš spojitou křivkou, je ještě méně.

A ani tak nelze najít původní předpis jinak, než hádáním.

Sofistikovanější metody používané v praxi - jako třeba SVM - najdou polynom nekonečného stupně.

Ale výsledkem jsou nesmírně komplikované funkce, které spočítá jen počítač.

Další sofistikovaný algoritmus používaný v praxi - neuronové sítě - vytvoří funkci, která třeba jen pro slušnou aproximaci funkce sin(x) bude vyžadovat stovky koeficientů.

Nejjednoduššími postupy pro hledání lineárních funkcí se ve statistice zabývá lineární regrese, ve strojovém učení potom polynomiální regrese a její varianty lasso nebo ridge regression.

Zdar chlapi, Tomáš má velkou pravdu, ale z toho co napsal bych na vašem místě dostal depresi, takže vám dám trochu naděje. To, co tady teď napíšu se dá relativně dobře použít za následujících předpokladů:

1. Nutný předpoklad: Nechcete být naprosto rigorózní, matematicky přesní, a neprůstřelní.
2. Pomůže když: víte jak ta naměřená data vznikla. tedy co to je za veličinu. A máte tedy alespoň přibližnou představu o fyzikální podstatě. To Vám totiž umožní vyvarovat se chyby typu že si zvolíte špatnej typ funkce.
3. Dá se to použít spíš pro tzv interpolaci, nikoli extrapolaci. Zkrátka... máte naměřený nějaký hodnoty, tak to proložíte nějakou funkcí, která tam bude sedět. Ale musíte být opatrní k čemu jí pak použijete. pokud jí použijete na dopočítání nějakých hodnot uvnitř toho intervalu kde máte naměřená data, tak je to OK. Ale určitě bacha na nějaké extrapolace, nebo předpovídání hodnota někde daleko od oblsati kde máte naměřený data.

No a teď ten postup. opakuji (pro Tomáše, kterej by mě určite nejradši zastřelil) nerigorźní postup:

1. kouknu na ten graf a tipnu si co by to mohlo být za funkci. Tady to vypadá na logaritmu nebo nějakou odmocninu. Samozřejmě je potřeba nechat tý funkci dostatek volných parametrů. pokud znám fyzikální podstatu, tak bych měl z teorie znát alespoň ten typ funkce.
2. Proložím ty body tou mojí funkcí a například metodou nejmenších čtverců najdu optimální hodnoty parametrů, aby ta křivka co nejlíp seděla na naměřená data.
3. Spočítám spolehlivost regrese a když je dobrá tak jsem spokojenej, když je špatná, asi jsem si zvolil špatnou funkci. Nebo mám málo volných parametrů, nebo jsou blbý data, nebo všechno dohromady :-). No tak zkusim jinou funkci. Jak píše Tomáš, je to o zkušenosti.

Tohle je takovej praktickej přístup statistika gangstera nebo většiny inženýrů :-).

:-))) hezky, Marku, ale i přesto s tebou Tomáš naprosto souhlasí, viz moje předchozí odpověď:

Spočítat to jde, ale pokud máš takhle málo dat, tak je nutné vědět, odkud data pochází, co má funkce vyjadřovat i jak se má používat. A nakonec je to hodně práce, protože se taková funkce dlouho hledá.

V práci dělám ještě větší prasárny, když se takovou funkci snažím najít.

Jen pro představu, do funkce vstupuje F 10.000 proměnných a vystujuje cca 3.000 proměnných, já hledám nejlepší funkci G, která odpovídá zadanému modelu, který je nekompletní a obsahuje chyby.

To je relativně malá funkce, obvykle bývají vstupních proměnných miliony.

Ou, díky z té první odpovědi jsem trochu depresi dostal, pravda :D ... já si myslel, že alespoň na nějaké jednodušší aplikace, kde je závislost jen pár proměnných (jak jsem klasicky z matematiky zvyklý), že existuje na to nějaká obecná disciplína matematické analýzy, to co popisujete vy jsou spíše experimentální postupy, ale chápu to ...

Uvedený graf neberu moc v potaz, je fakt hodně chudý na data.

Mikoláši, když se studenti učí analýzu, tak mají tendenci dělat ukvapené závěry, kdy odhadují limity funkcí bez důkazu, udělají nákres funkce bez znalosti derivace nebo chování v krajních bodech... a skoro vždycky se spletou :-P. Ono to nějak nejde dokonce ani tímhle směrem, kdy funkci znáš.

Obecné disciplíny, které se tímhle zabývají, jsou Statistika a Strojové učení, což už samo o sobě napovídá, že to nebude sranda - a není. Statistika vezme data a hledá model, který ta data mohl vytvořit. Strojové učení je o hledání obecnějších funkcí pro větší množství dat, a ačkoliv jsou základy statistické, přístup bývá obvykle spíše empirický. Empirický důsledek použitelnosti strojového učení spočívá v tom, že není důležité přesně trefit funkci, ale jen a pouze zda máš dostatek dat.

Další obory, které mají podobné zájmy, jsou kryptografie a kryptoanalýza. V kryptografii se snažíš vytvořit funkci, pro kterou nepůjde nalézt původní předpis, zatímco kryptoanalýza se snaží předpis hledat. A obě strany mají extrémně těžkou práci. Například jedna z šifer - DES - je velice složitou kombinací desítek funkcí a stovek operací. Její slabost spočívá v tom, že jedna z jejích podfunkcí je skoro-lineární, díky čemuž byla rozbita.

Nebo Teorie her je sociálně-ekonomicko-statistická disciplína, která hledá modely (funkce) pro vysvětlení a předpovědi chování nebo událostí. Dá se odhadnout směr, kterým fotbalista kopne penaltu? Nebo odhadnout chování firem na trhu nebo prasat u koryta? To jsou pikantnější příklady funkcí, kterými se teorie her zabývá.

Proč je to všechno tak komplikované?

No, ty funkce, které znáš "klasicky z matematiky", jsou ekvivalentem kostiček, se kterými si hrají dvouleté děti.

Jsou to schválně hezké a jednoduché funkce, abys pochopil téma s ukázkovými příklady k řešení.

Ale z toho dům nepostavíš a v praxi je většina funkcí řádově složitějších, takže by takový obor, na který se ptáš, vlastně neměl moc smysl.

Deprese? :-D

Ale ne, tyhle obory, o kterých mluvím, jsou neskutečně zábavné.

Díky za odpovědi, ale vůbec se mi nelíbí =D měl jsem naději, že něco takového existuje :D chtěl jsem něco takového použít, pro jednoduché závislosti, které se objevují v astronomii, třeba světelné křivky proměn hvězd, nebo vícehvězdných systémů. Představoval jsem si, že mi matematika dá prostředek, kterým by mi byla schopná dát nějakou předpověď, nebo spíše typ na to, co způsobuje ty změny jasnosti. Předpokládal jsem, že na základě tohoto by se ty křivky daly nějak rozumně analyzovat, aby mi alespoň prozradily jestli je tam těch hvězd více než jedna. Napadlo mě to, protože dosud se to dělá právě metodami pokus omyl, což mě k téhle myšlence vyprovokovalo.

Mám v knihovně 5 dílů Mathematical Astronomy Morsels od Jeana Meeuse a Colwellova Řešení Keplerových rovnic, přečti si něco z toho, abys viděl, jak vypadají vzorce od profesionála. :-) Dokonce ani já nevím, kam na to Meeus chodí.