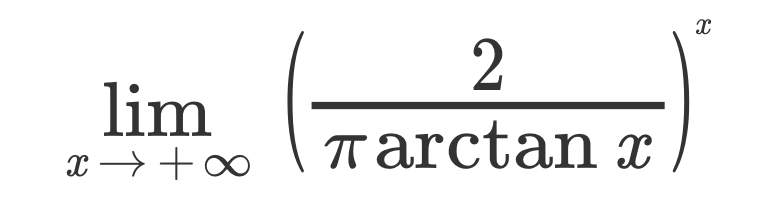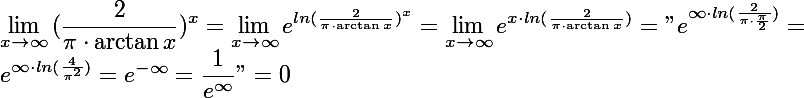Limita funkce

Není to zapsáno úplně formálně správně, ale postup snad vidět je.

Ahoj Romane,

stačí použít znalost inverzních funkcí. V našem případě to může být funkce e^x a ln(x) . Funkci (2/pi arctg(x) )^x si přepiš jako e^(ln(2/(piarctg(x)))^x) (můžeme to tak přepsat právě kvůli tomu, že ln(x) a e^x jsou vůči sobě inverzní a vyrušilo by se nám jejich působení) a následně použiješ znalost součtu logaritmů. Víš, že : ln(x^r)=rln(x), tak to aplikuj na tvůj logaritmus v exponentu. Pak už spočítat limitu je jednoduché. Výjde 0.

To je zbytečně komplikované.

pro x > 1 je atan(1) > 2/pi

=> 2/(pi * atan1) < 1

=> vyraz v zavorce je mensi nez 1 a klesajici, x>1 roste a mocnina je take klesajici

=> pro důkaz stačí najít jednoduchou funkci větší než výraz, to plati pro (2/pi)^x

=> 0 < limita < (2/pi)^x -> 0 a věta o limitě sevřených funkcí

Skvělé! Děkuji Vláďo, Petře a Tomáši za vaše postupy řešení! :) Máte u mě všichni sušenku. Nakonec jsem uplatnil radu Vladana. Řešení, ačkoliv také není úplně formální, v obrázku.