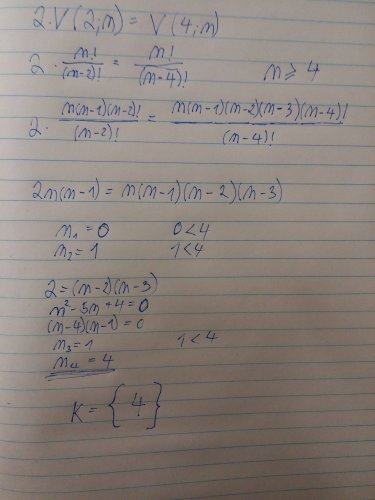Variace bez opakování
Ahoj, prosím nějakého matematika :-) o pomoc s následující úlohou (a vysvětlení postupu):
"Z kolika prvků je možné vytvořit dvakrát více čtyřčlenných než dvojčlenných variací?"
Řešení by mělo začínat jako rovnice: 2 krát V(2;n) = V(4;n)
Díky moc!
Káťa M.
07. 02. 2016 19:48
1 odpověď
Ahoj Káťo,
stačí si uvědomit, jak jsou definovány variace. To je nutná znalost při výpočtu těhle rovnic. Takže, mějme sestavenou rovnici. Nejprve určíme def. obor rovnice, protože neni faktoriál definován pro záporná čísla, tak musí platit n=>4, kde n je nějáké přirozené číslo. Teď nám jde o to, snažit se ji co nejvíce zjednodušit. Vidíš, že ve jmenovateli i čitateli jsou faktorialy, těch se chceme zbavit, proto rozvineme faktorial v čitateli, tak, aby se nám následně vykrátily. Po vykrácení faktorialu máme rovnici čtvrtého stupně, která má na první pohled kořeny 0,1. Ani jeden kořen nevyhovuje naši podmínce, tak hledáme zbylé dva, rovnici vydělíme n(n-1) (víme, že n ani n-1 není 0, proto můžeme beztrestně dělit) a dostáváme kvadratickou rovnici, jejíž kořeny jsou 1 a 4. 1 jsme tu už měli, ta je nevyhovujicí, ale 4 je v def. oboru, proto má rovnice jediné řešení a to n=4.