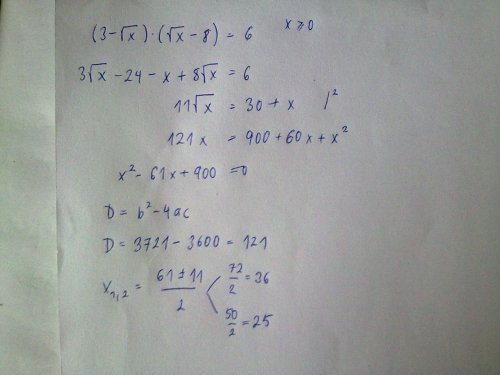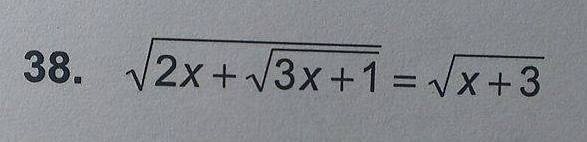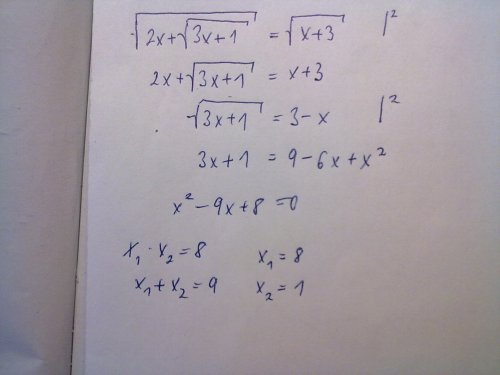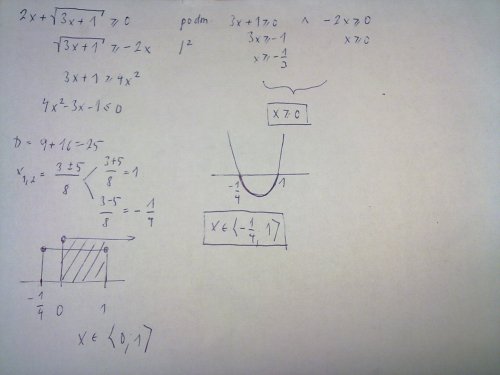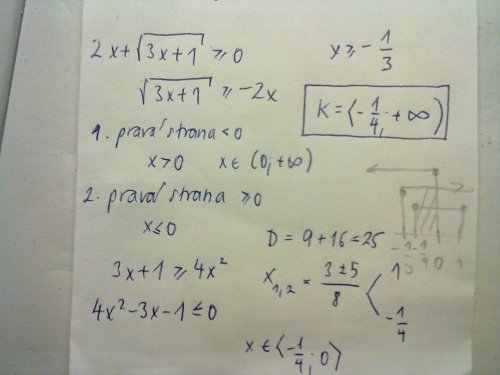Iracionální rovnice

Dobrý den, na obrázku posílám řešení, ještě by se měla dělat zkouška (tu tam napsanou nemám), ale oba kořeny splňují podmínku x ≥ 0 (a navíc to myslím vychází i po zkoušce).

Jo super, děkuji moc :)

A můžu ještě poprosit o pomoc s tímto příkladem? Výsledek má být 1, ale ať se snažím sebevíc, vychází mi stále jiná čísla nemůžu se k tomu dopracovat :/

Pro jistotu poprosím i o ten další obrázek :)

Řešení rovnice je zde, ale popravdě řečeno si teď zpětně nejsem úplně jistá těma podmínkama, co jsem vám psala v minulém příspěvku. Takže si s radou radši počkejte na někoho, kdo vám to dovede vysvětlit správně. ;)

To je trošku složitější, nejdříve si musíte udělat podmínky z obou stran rovnice. Na obrázku posílám podmínky z levé strany rovnice, tzn. z té velké odmocniny (snad to jde přečíst a je to aspoň trochu srozumitelné). Pro odmocninu platí, že výraz v ní musí být ≥ 0. Takže vlastně dostanete nerovnici s odmocninou, u které, pokud ji chcete vypočítat, musíte opět udělat podmínky, a to tak, že musí být obě strany ≥ 0. Pak už můžete umocňovat, vyjde kvadratická nerovnice, jejíž kořeny opět vymezují určitý interval. A pokud spojíte oba intervaly dohromady, vyjde podmínka, která vymezuje, že x může být pouze z intervalu od 0 do 1.

Poté už normálně spočítáte tu původní zadanou rovnici (nejdříve umocníte obě strany, poté převedete 2x na pravou stranu, opět umocníte, tím zmizí i poslední odmocnina, a poté už jen dopočítáte kvadratickou rovnici). Mně vyšly kořeny 8 a 1, ale 8 být správný nemůže, protože podle podmínky má být x v intervalu od 0 do 1, takže správné řešení je pouze 1. (kdyby bylo potřeba, můžu dodat obrázek)

EDIT: Tak ne, omlouvám se vám, když nad tím tak přemýšlím, tak to -2x ≥ 0 je myslím špatně, (protože když tam dosadíte za x např. -(1/6), tak ta nerovnice vyjde správně, takže ta čísla očividně nemusí být nezáporná). Dost jsem se do toho zamotala, takže prosím někoho, kdo tomu opravdu rozumí, o pomoc.

I tak moc děkuji :)

Vůbec není zač ;) Možná, pokud to bude iracionální rovnice (a ne nerovnice), neřešte podmínky, tu rovnici prostě vyřešte, a pak ty výsledky pouze zkontroluje pomocí zkoušky (protože zde opravdu vyjde, že pro x = 1 rovnice platí, a pro x = 8 rovnice neplatí.

Ahoj Martino a Kláro,

jen doplním, že podmínky jsou špatně kvůli špatně vyřešené iracionální nerovnici, kde už se ty podmínky mají právě řešit a hlavně rozdělovat případy, kdy je umocnění ekvivaletní a kdy ne :-)

Tak jo, promiňte, že to ještě otvírám, ale je ta nerovnice teď vyřešena správně? (je to dost nepřehledné, řešení je to K vpravo)

Mně to vyšlo stejně :-)