Numerické myšlení_1

Ahoj, napadlo mě ten první příklad popsat rovnicí a využít principu fungování desítkové číselné soustavy. V příloze posílám návrh možného postupu řešení. Nevím, jestli je to dobrá myšlenka, ale teoreticky se mi povedlo z toho vyjádřit funkci, která popisuje, jak máš zkoušet dosazovat čísla a jak z toho dostat množinu možných příkladů, které hledáš.

Trochu tomu nerozumím.

Jen poznámka.

Správná odpověď je : V prvním výpočtu je - , a ve druhém je také -

Patriku, ukážu ti, jak vyřešíš první příklad, druhý se dělá podobně.

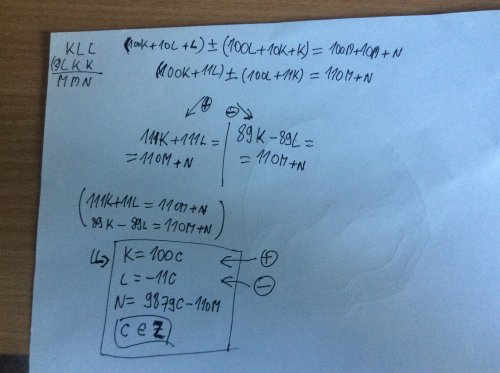
Máme RŮZNÉ číslice KLMN:

KLL

LKK

MMN

Co kdybychom zkusili sečíst KLL+LKK?

Poslední sloupec říká, že L+K=N, ale předposlední říká, že L+K=M.

To znamená, že L+K je větší než 10, abychom mohli přenést jedničku doleva a dostali různé součty M a N.

Jenže první sloupec je L+K=M a pokud přeneseme jedničku, dostaneme 1MMN a to podle zadání není možné.

Takže správná operace je odčítání a sčítání není možné, protože bychom potřebovali 1 navíc.

Druhý příklad se řeší prakticky stejně.

V úkolu to nemáš, ale mnohem zajímavější je najít všechna řešení.

Pro zábavu si to zkusíme, když jsi sám uvedl "numerické myšlení" v názvu.

Máme KLL - LKK = MMN, ale prostřední číslice jsou tam zbytečné.

Stačí řešit: KL

-LK

=MN

Podle posledního sloupce je L - K = -N, takže K - L - N = 0.

M musí být M = N-1, protože K>L podle prvního sloupce.

Teď uděláme rovnici: 10K + L - 10L - K = 10N - 10 + N 9K - 9L = 11N - 10 9(K - L - N) = 2N - 10 0 = 2N - 10

N = 5

K = L + 5

Dostali jsme KLL

-LKK

=455

A protože K = L + 5, existují jen 3 řešení:

611

-166

=445

722

-277

=445

833

-388

=445