Test generátoru náhodných čísel - exponenciální rozdělení
Zdravim.
Dostali jsme za úkol otestovat generátor náhodných čísel (například ZXSpectrum). A máme zjistit nejmenší vzdálenost mezi všemi páry. Ta vzdálenost podléha exponenciálnímu rozdělení.
Náhodné body mám vygenerované, nejmenší vzdálenost mezi všemi páry též.
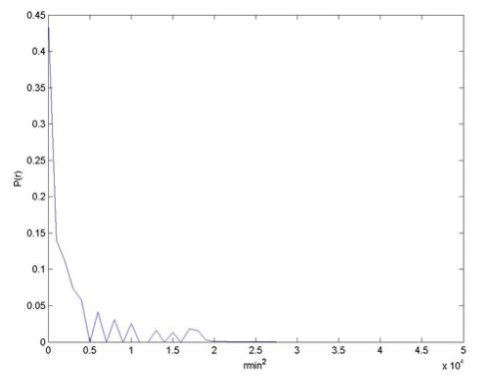
Ale nemám ponětí jak přistupovat na vykreslení toho exponenciálního rozdělení. V příloze je obrázek - mělo by tak vypdat to expnenciální rozdělení právě pro generátor ZXSpectrum.
Jak mám však dosáhnout podobného grafu, pokud zatím mám pouze pole těch nejmenších vzdáleností? Pokud chci vykreslit nějaké rozdělení, potřebuju nějakou pravděpodobnost výskytu jednotlivých vzdáleností, že?
Budu vděčný za každou radu!
Felix Š.
08. 05. 2016 15:01
1 odpověď
Felixi, abych se přiznal, tak moc nechápu, co máš za úkol nebo kde je problém?
Jestli testuješ Lehmerův generátor, tak to je cyklická grupa Z[n]* s n=2^16+1 a generátorem g=7^5 ve tvém případě.
Minima vzdáleností na cyklické grupě budou dvojice hodnot vzdálené 1 až n/2 s uniformním výskytem, kde jsi vzal exponenciální distribuci?
A ten obrázek vypadá, že ho generovalo R.
V tom případě je na ose x seřazená distribuce čtverce vzdáleností a na ose y jsou pravděpodobnosti jevů.
Takže si vezmeš frekvence vzdáleností F, F[i^2]<-frekvence vzdalenosti i^2, pak uděláš normu přes velikost univerza.
plot(F / sum(F) , type='l')
Alternativně mě napadá, že pokud neuděláš test korektně, dostaneš triangulární distribuci místo uniformní.
Kvadrátem vzdáleností získáš transformaci osy x a vypadá to jako exponenciální, i když je to kvadratická transformace.