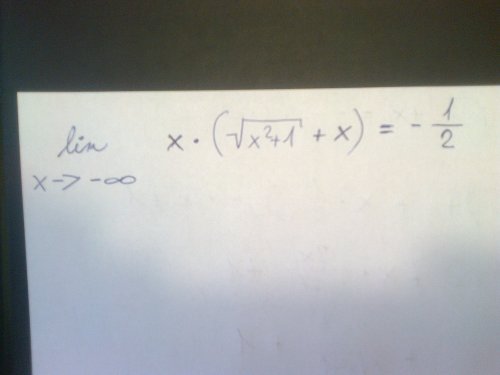Limita funkce

Ahoj Davide,

daný výraz bych rozšířil výrazem sqrt(x^2 + 1) – x, vznikne nám [x*(sqrt(x^2 + 1) + x)(sqrt(x^2 + 1) – x)] / [sqrt(x^2 + 1) – x]. Nahoře je vzorec (a + b)(a – b) = a^2 – b^2. Bude to tedy [x*(x^2 + 1 – x^2)] / [sqrt(x^2 + 1) – x] = [x] / [sqrt(x^2 + 1) – x]. Nyní ve jmenovateli z toho, co je pod tou odmocninou, vytkneme x^2 ... tedy x / { sqrt[(x^2)*(1 + 1/(x^2)] – x} = x / [|x|sqrt(1 + 1/x^2) – x]. Vrátíme se k tomu, že řešíme limitu a protože x jde do minus nekonečna, tak x "bude záporné číslo" a tudíž |x| = –x. Řešme limitu: lim pro x –> –oo z x / [–xsqrt(1 + 1/x^2) – x], dole vytkneme x a pokrátíme: lim pro x –> –oo z 1 / [–*sqrt(1 + 1/x^2) – 1], kde 1/x^2 jde k 0 a "vypadává ze hry", takže výsledek bude 1 / [–*sqrt(1) – 1] = 1 / (–1 – 1) = – 1 / 2. S formulací té absolutní hodnoty si nejsem vůbec jist :-)

Děkuji moc za pomoc a čas:)