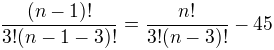Kombinatorika (n-4)!, ...
Dobrý den,
usilovně se snažím rozlousknout dvě úlohy, bohužel si už ale nevím rady.
Zadání úlohy č. 1:
Zmenší-li se počet prvků o jeden, zmenší se počet kombinací třetí třídy z nich vytvořených bez opakování o 45. Určete počet prvků.
Můj postup:
Vytvořil jsem si rovnici
C3(n)-45 = C3(n-1)
Došel jsem k (příloha č. 1) a dál si nevím rady kvůli (n-4)! a jeho následnému rozvinutí.
Zadání úlohy č. 2:
Kolik je prvků, jestliže počet variací čtvrté třídy z nich vytvořených bez opakování je třicetkrát větší než počet variací druhé třídy z nich vytvořených bez opakování.
Opět jsem si vytvořil rovnici:
V4(n):30 = V2(n)
a dopracoval jsem se opět k rozvinutí až do (n-4)!. Dále jsem si opět nevěděl rady, vznikne mi totiž po vykrácení faktoriálů n*(n-1)(n-2)(n-3) a z toho nebude kvadratická rovnice.
Předem velice děkuji! :-)
Filip K.
14. 06. 2016 16:25
2 odpovědi
Filipe,
k tomu prvnímu: normálně ten n-1 faktoriál rozviň až do n-4 faktoriálu. vyleze ti tam sicen na třetí, ale na pravé straně rovnice taky, takže se ti odečtou a dostaneš kvadratickou. Prostě se toto neboj, roznásob to a bude to OK.
U tý druhý rovnice bych si tipl takhle z hlavy, že ti vyleze rovnice 4. řádu, která ale bude obsahovat pouez sudé mocniny n a tudíž ji substitucí převedeš na kvadratickou. Ale takhle z hlavy si tím nejsem úplně jistej. Schválně kdyžtak napiš, jestli to tak vyšlo.
Ten první příklad vyšel - super! :-) Hrozně moc děkuji, bál jsem se právě toho n na třetí a ono se to pak vážné vykrátilo.
Ten druhý příklad vyšla rovnice:
http://rogercortesi.com/eqn/tempimagedir/eqn3282.png - jak teď udělat substituci? Nemáte na to nějaké video? :-) Ještě koukám, že jsem zapomněl *30
Ještě jednou moc děkuji