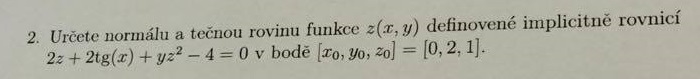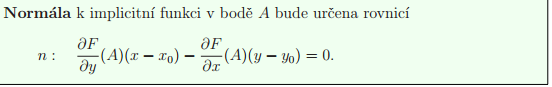Určení tečné roviny a normály
8 odpovědí
Postupu rozumím, jen mě zajímá ten konkrétní vzorec, který použiji, pokud jsou zadány 3 proměnné a hledám normálu :-)
Říká ti něco pojem gradient funkce ? Nebo se mám něják obejít bez toho ?
Gradient používám při stanovení derivace ve směru, takže vím že se sestavuje z parciálních derivací.
Tečná rovina je tedy množina bodů (x,y,z) splňující : gradient f(A) . ( x-x0 , y-y0 , z-z0) = 0 nebo po úprávě : fx(x-x0)+fy(y-y0)+fz(z-z0)=0 , kde fx,fy,fz jsou parcialní derivace podle jednotlivých proměnných.
A pro zjištění normály pouze dosadím parciální derivace do normálového vektoru?
Gradient je normálový vektor ke grafu té funkce v bodě A , takže stačí spočítat gradient.
Ahoj Vlasto,
jen spočteš první derivace podle x,y a z a vše, co znáš, dosadíš do jednotlivých vzorců a je hotovo. :)