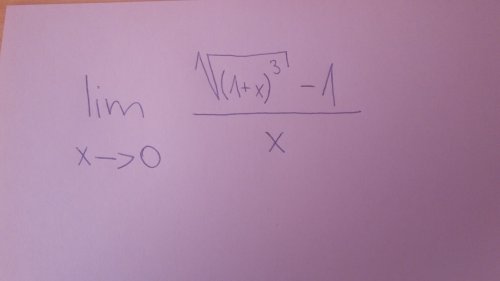Limita
Ahoj, minule jste mi poradili, tak se na vás znovu obracím. Nevím si rady s touto limitou. je to typ 0/0. zkoušel jsem rozšiřování ale pořád je to nula/nula. poradíte? dík
...teď mě ještě napadl L´H ale rád bych věděl jestli a jak to jde udělat tím rozšířením zlomku
Pepa V.
26. 08. 2016 20:35
5 odpovědí
Ahoj Pepo,
a můžeš ještě vyfotit a poslat tvůj vlastní postup, když jsi zkoušel to rozšiřování, čím si tedy rozšiřoval, co vyšlo po úpravě, atd. :-)
Došel jsem k závěru že rozšíření zde není možné protože nám to hodí odmocninu do jmenovatele (obrázek) což je ještě horší, takže takhle asi ne
pak mě napadlo rozdělit to zadání na dva zlomky kde bude jmenovatel x , ale co dál? nebo nějak uplatnit toho L´Hopitala? jak?
rád bych se dozvěděl oba způsoby řešení tedy použitím L´Hopitalova pravidla a pak bez něj. já fakt nevím, poradíte někdo? :-)
To, že je odmocnina ve jmenovateli, nám nutně nevadí. Zkusil bych "roznásobit" tu závorku (1+x)^3 ve jmenovateli podle vzorce (a+b)^3 a zkoumat, co se stane v tom jmenovateli :-) Pokud si nepamatujete ten vzorec, tak bych použil: (a + b)(a + b)(a + b) = (a + b)^2*(a + b) = (a^2+ 2ab + b^2)*(a + b) ... po roznásobení získáme daný vzorec :-) L'Hopitala používáme tak, že zderivujeme čitatel i jmenovatel a limita zůstane stejná (samozřejmě pouze za určitých podmínek, typy 0/0, atd.)
Už to mám. výsledek je 3/2. A bylo to jednoduché :D odmocnina ve jmenovateli nevadila a použil jsem (a+b)^3 .
Mám to vypočítané i L´Hopitalem. po derivaci: 3/2(1+x)^2 ...tam jsem dosadil 0 a vyšlo těch 3/2
Jestli je to dobře...díky Martine
Přesně tak, při rozšíření se jedničky odečetly a šlo krátit x. Ta derivace by ale podle mě měla spíše vyjít 3/2 * (1+x)^(1/2), ta limita ale vyjde stejně :-)
Není zač, Pepo! :-)