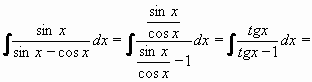Úprava před integrací

Ahoj Martine,

a jak si dospěl k tomuto výsledku? Míním to 1 – tg(x).

Dělal jsem to sin(x)/sin(x) - sin(x)/cos(x)

Ono to k tomu svádí, ale obecně určitě neplatí a/(a + b) = a/a + a/b = 1 + a/b neboť 1 + a/b se společným jmenovatel se rovná (b + a)/b = (a + b)/b. V našem případě je a = sin(x) a b = –cos(x). To by také šlo tvrdit, že 10/(10 – 5) = 10/10 – 10/5 = 1 – 2 = –1 ... to je nesmysl. :-)

Jj pak jsem věděl, že je to blbost, ale nevím jak dál co se týče goniometrických výrazů.

Osobně bych využil té úpravy na tg(x)/(tg(x) – 1) a použil substituci tg(x) = t.

Ano, ale jak se k tomu přišlo k těm úpravám, dělení polynomů taky není dobrá cesta.

Zde je potřeba si prostě všimnout, že když te zlomek rozšíříme 1/cos(x) (čitatel i jmenovatel vydělíme cos(x)), tak nahoře nám vznikne tg(x), dole také plus 1. Neexistuje žádný univerziální postup, je potřeba to buď hned uvidět, nebo zkoušet nějaké úpravy (vzorce, to rozšiřování), a to tak dlouho a tolikrát, dokud nám z toho nevyleze něco "příjemnějšího". :-)

Jako sin(x)/sinx-cosx krát 1/cosx?

Musíme ale tím 1/cos(x) vynásobit (je to to samé jako dělit cos(x)) jak čitatel, tak i jmenovatel abychom nezměnil hodnotu výrazu. Další postup, o dost rychlejší a nejspíš i lepší, který jsem si prvně neuvědomil, je vyjádřit si jednu z těch funkcí (sinus nebo cosinus) jako tangens ze vztahu sin(x)/cos(x) = tg(x) a dosadit do výrazu, kde pokud se to dá napsat jen pomocí tangenty, tak by ta "druhá" funkce měla vždy vypadnout.

Vrátím se k tomu ráno, jsem z toho vážně jelen :) ještě se ozvu a jinak díky

Aby se nezměnila hodnota výrazu, smí se výraz násobit nebo dělit jen jedničkou. Ale jednička může mít mnoho podob. A tady je jednička zastoupená cos x/ cos x což je vlastně taky jedna. Tím pádem je ta úprava vyjde podle obrázku. Tedy jestli tímto směrem byla pokládána otázka.. :)

Děkuji. Valášek mi to vysvětlil srozumitelně, mám to udělat tak, že si rozšířím vydělením čitatele i jmenovatele cos(x). Věděl jsem rozšířování zlomků pouze bez goniometrických výrazů. Proto jsem z toho byl jelen. Na internetu nebyla o tom ani zmínka rozšiřování zlomků goniometrických výrazů.

Jinak díky za snahu a radu :)