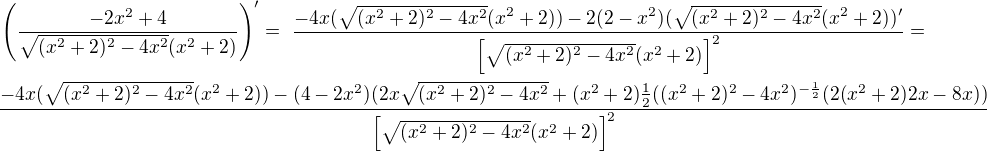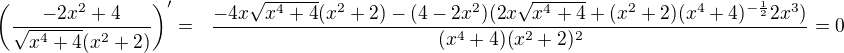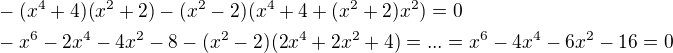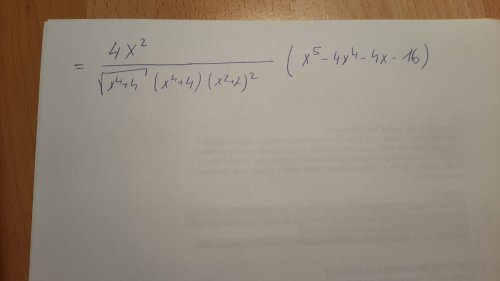Úprava druhé derivace
Zdravím všechny - mám vyjádřenou druhou derivaci a nevím si rady s tím, jak ji správně upravit, tak aby se mi dobře počítali vlastnosti funkce (inflexní body, konkávnost, konvexnost).
Mohl by mi někdo s úpravou derivace pomoct, nebo s tím jak rychle určím vlastnosti v této derivaci.
Původní funkce:
arcsin((2x)/(x^2+2))
Druhá derivace
Tomáš M.
22. 11. 2016 01:41
12 odpovědí
Tomáši, mordoval jsem se s tím dneska asi dvě hodiny a vyšlo mi to čtyřikrát jinak :-).... Ještě to zkusim :-)...
Díky moc za snahu, já teda taky zkouším - ale nedaří se. Je to pro mě poslední věc, která mi chybí k určení grafu funkce.
Ahoj, mně osobně vychází úprava na zlomek, ve jmenovateli je (x^2+2)^2odm(x^4+4)(x^4+4) a v čitateli je 4x(x^6-4x^4-4x^2-16). Takže v nule by mohla nastat inflexe, další dva kořeny čitatele (další body podezřelé z inflexe) lze zjistit jen řešením kubické rovnice po substituci x^2 = a, ale nevychází to hezky :-)
Jo, tak to mi vyšlo taky. nula a kubická rovnice :-)...
Můžete mi prosím poslat ten postup, jak jste se dostali k té nule a kubické rovnici (tu samotnou úpravu zlomku) - protože tam jsem já pohořel xD. Já jsem se nedostal ani k tomu tvaru, jako máš ty Martine :D
Jednak ve výrazu pod odmocninou lze umocnit podle vzorce a upravit, v čitateli se umocnuje na -1/2, což znamená umocnovat na 1/2 převrácenou hodnotu, tedy odmocnovat převrácenou hodnotu. Tady bych použil společný jmenovatel, poté už jen roznásobení a posčítání příslušných mocnin. Spíše ty pošli svůj postup :-)
Já jsem to teda řešil tak, že jsem si upravil první derivaci na tvar v obrázku, vynásobil jsem to odmocninou z
(x na 4+4) a vydělil jsem to 4x.
Upravil jsem a získal jsem tohle.
Bohužel to nevychází :D Rozepsal bych to víc, ale na papíře to po mně nejde přečíst xD.
Dělit a násobit rovnici můžeme jen číslem různým od nuly. Pokud by výraz, kterým dělíme(násobíme), mohl být nula pro nějakou hodnotu, musíme tuto hodnotu vyšetřit zvlášt, nejlépe takovým výrazem vůbec nedělit. Výrazem odm(x^4+4) ale vynásobit můžeme bez starosti, proč? Ale tím vydělením 4x totiž "ztratíme" kořen x = 0. Jinak v té úpravě mi přijde, že je chyba .... –(4–2*x^2) ...?...–(x^2–2) ???
Jo díky moc za rady, zkusím to znova - snad už to půjde :D
Tak jsem se kousnul a dotahl jsem to do nejakeho rozumneho tvaru. Teda ne ze by tam ten polynom pateho radu byl nejakej super, ale odsud dal uz je videt co je potreba. Jo a mam to malilinko jinak, tak nevim... snad je to dobre.
Dokonceni
