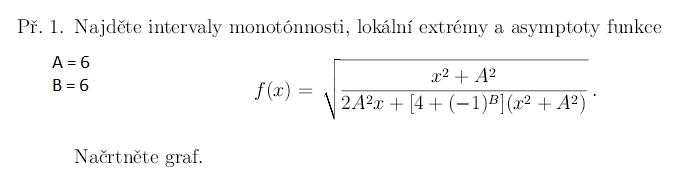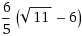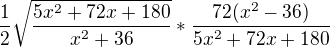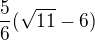Průběh funkce -

Ahoj Patriku, pokud nemáme řešit obecně, tak bych dosadil za A a B dané hodnoty a provedl bych první derivaci, pak zkoumáme, kdy je první derivace nulová (možné extrémy - musíme ověřit druhou derivací a dosazením) a kdy je derivace kladná (rostoucí), záporná (klesající).

Ahoj Patriku, pokud se to chceš naučit, doporučuju zakoupit tento kurz: http://mathematicator.com/index.php?page=kurzy&a=1

Je tam detailně vysvětleno vše co potřebuješ.

Problém nejspíš bude že jsem se zalekl hned na začátku, u definičního oboru.

Proto se zeptám zdá je to správný definiční obor jak pro + tak pro -, a zda je to vše?

A plus ktomu jak bude vypadat 1 derivace, funkce ve funkci, ale jak to sepsat.?

Děkuji za pomoc

A první derivace výsledek vypadá takhle?

Nemělo by těch (5x^2+72x+180) v tom druhém zlomku být na druhou, derivoval se podíl ne?

Ano na druhou, no jak z tohoto nebo jak to ještě upravit a vyčíst stacionární bod?

Nevím co dělám špatně

Do těch racionálních mocnin bych se nepouštěl, nechal bych to v těch odmocninách a druhých mocninách. Zkoumáme, kdy bude první derivace nula, je tam nějaký zlomek. Kdy je zlomek roven nule? P.S. Nemůžeme psát, že první derivace funkce se rovná funkci a derivovat to až po pár rovnítkách :-) Tu čárku (derivaci) tam musíme pořád psát. To je jen taková malá hnidopišská :-)

No já už jsem z toho tak zmaten že bych potřeboval vědět co jak to má vůbec být.

Nenapsal byste mi to byl byste laskav.

Děkuji za vstřícnost.

Zlomek je nulový tehdy, když čitatel je nulový (a jmenovatel je nenulový - tady bude vždy nenulový), takže když x^2 – 36 = 0 a když 5x^2+72x+180 = 0. Tu druhou rovnici nemusíme řešit, protože jsme je řešili při Df, tento výraz nula být nemůže, protože jím dělíme v té funkci.

Definiční obor je tedy celý zlomek větší 0, řeším pomocí nerovnici.

Teď jak vyřešit (poprosil bych o postup) 1. derivaci.

vím že se jedná o složenou funkci, ale nevím jak to řešit a sepsat rozumně.

Ted nevím, na co se ptáš. Jak vyřešit 1.derivaci, tím myslíš, kdy je nulová?

Derivaci mám ale řeším definiční obor jde mi o to jak to rozumně napsat

Zlomek pod odmocninou má být větší nule a co dál jak to vyřešit

Jak vyřešit tu nerovnici se ptáš?

Ano , protože vím o co se jedná ale nevím jak tenhle případ vyřešit

Http://mathematicator.com/index.php?page=play&a=329 To by mělo pomoct

Takže stačí vyřešit dane nerovnice jmenovatel větší 0?

V našem příkladě ano, protože x^2 + 6 bude vždy kladné, mimochodem proč?

No a vyjde mi +- příloha to ale asi není výsledný def obor

5/6(odm11 - 6) je číslo, jak si na něj přišel a co vyjadřuje?

To číslo je nebo mělo být řešením kvadraticke rovnice v jmenovateli

A když dáme - nekonecno to číslo) (to číslo nekonečno) mělo být definičnim oborem?

Proto se ptám, jak si přišel zrovna na tohle číslo, protože tohle číslo není kořeném té rovnice 5x^2 + 72x + 180 = 0.

Jak ne? (-72 +-odmocnina 1582)/10.

Z odmocniny udělám 12odmocnina11 a 12 vytknu a zkrátím 2

Co? A proč?

No je to spravne nebo ne?

Jak si to poslal podruhé, tak tam je to právě špatně, má tam být těch 6/5, jak to máš prve.

Promin, měl jsi to už na tom minulém papíře a předtím jsi to také posílal, ano je to tedy 6/5*(+–odm(11) – 6).

No a tedy celkový definiční obor tedy bude vypadat jak?

Vyšly tedy dva kořeny a Df bude (-oo; menší kořen) U (větší kořen; +oo). Kolik je menší a kolik je větší kořen?

Menší je s + a větší s - a jak to zapsat?

Tak jak píšu výše, jen místo menší kořen napíšeš to číslo, to nevadí, že je trochu složitější.

Snad poslední otázka, při řešení intervalu monotonosti musím zahrnout jak stacionární bod tak i z podmínky?

A dosazovat do první derivace? A tím zjistím zda roste nebo klesá?

Pokud vím, tak funkce je klesající tam, kde je první derivace záporná a rostoucí tam, kde je kladná, zase nějaké nerovnice. Ve stacionárních bodech může být extrém, ale také nemusí, pak tam roste, nebo klesá.

A do těch nerovnic je třeba dát intervaly jak řešení definiční oboru a stacionární bodů

Promin, nerozumím otázce.