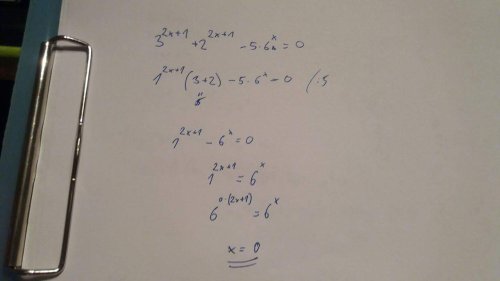Rovnice s mocninami

Smysl to dává, ale jinak je to úplně špatně :-) Vytýkáš tam 1^(2x+1), po zpětném roznásobení s tím (3+2) by tam bylo 31^(2x+1) + 21^(2x+1), což rozhodně není 3^(2x+1) + 2^(2x+1). Když nějaké číslo umocnujeme, nemůžeme to číslo vynásobit nějakým jiným, např: 5*(3^x) se rozhodně nerovná 15^x. Nula je sice řešením této rovnice, ale není jediným řešením, a je to čirá náhoda. Zkusil bych si napsat 3^(2x+1) jako 3^(2x) * 3^1. To samé u druhého členu a 6^x = (2*3)^x = 2^x * 3^x. Ted bych celou rovnici podělil (2^x * 3^x), zkus další vymyslet ty. :-)

Martine vyšlo mi x=5 tak snad je to dobré

Ne tak to je taky špatně

Nejlepší bude poslat postup, jak se přišlo na těch 5.

No je asi velká blbost vytýkat x z ty mocniny že jo

Samotné x určitě vytknout nemůžeme.